Question

A man rides a jet boat with a speed of $40km/hr$ in the north -east direction and the shore line makes an angle of ${10}^{\circ }$ south of east . Find the component of the velocity of the jet boat
(i) along the shoreline
(ii) perpendicular to the shoreline.

Explanation

To solve the problem, we need to find the components of the velocity of the jet boat along the shoreline and perpendicular to the shoreline. Let's break it down step by step.

Step 1: Understand the Directions
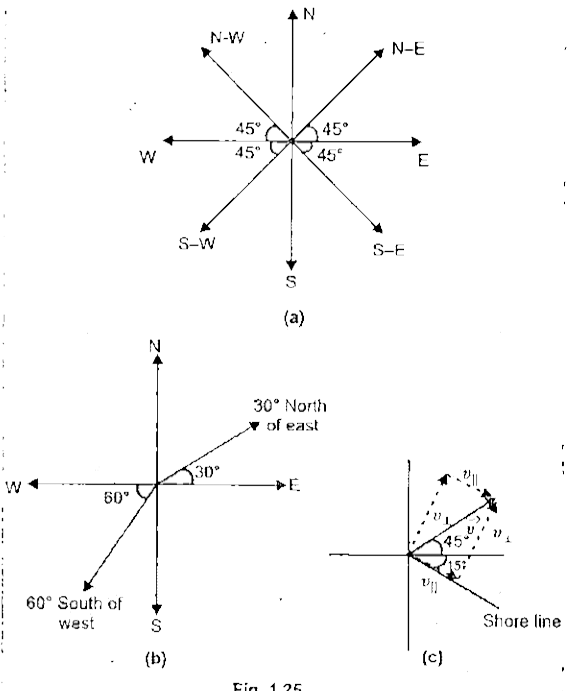
- The jet boat is moving in the North-East direction, which is at an angle of 45 degrees from the East.
- The shoreline makes an angle of 10 degrees South of East. This means the shoreline is at an angle of 10 degrees below the horizontal (East).

Step 2: Determine the Angle Between the Velocity and the Shoreline
- The angle between the North-East direction (45 degrees) and the shoreline (10 degrees South of East) can be calculated as:
\( \theta = 45^\circ + 10^\circ = 55^\circ \)

Step 3: Calculate the Components of Velocity
The velocity of the jet boat is given as \( V = 40 \, \text{km/hr} \).

(i) Component of Velocity Along the Shoreline
- The component of velocity along the shoreline (OB) can be found using the cosine of the angle:
\( V_{\text{along}} = V \cdot \cos(\theta) = 40 \cdot \cos(55^\circ) \)
- Calculating this gives:
\( V_{\text{along}} \approx 40 \cdot 0.5736 \approx 22.94 \, \text{km/hr} \)

(ii) Component of Velocity Perpendicular to the Shoreline
- The component of velocity perpendicular to the shoreline (OA) can be found using the sine of the angle:
\( V_{\text{perpendicular}} = V \cdot \sin(\theta) = 40 \cdot \sin(55^\circ) \)
- Calculating this gives:
\( V_{\text{perpendicular}} \approx 40 \cdot 0.8192 \approx 32.74 \, \text{km/hr} \)

Final Answers
- (i) The component of the velocity of the jet boat along the shoreline is approximately 22.94 km/hr.
- (ii) The component of the velocity of the jet boat perpendicular to the shoreline is approximately 32.74 km/hr.