A man rows a boat with a speed of 18Kmh−1 in the north-west direction (figure). The shoreline makes an angle of 15∘ south of west. Obtain the components of the velocity of the boat along the shoreline and perpendicular to the shoreline.

The north-west direction of the boat makes an angle of 60∘ with the shoreline .
component of the velocity of boat along the shoreline
=18cos60∘Kmh−1=9kmh−1
components of the boat velocity along a line normal to the shoreline
=18sin60∘Kmh−1=18×√32Kmh−1=9√3Kmh−1.
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.1
19 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
A man rides a jet boat with a speed of 40km/hr in the north -east direction and the shore line makes an angle of 10∘ south of east . Find the component of the velocity of the jet boat
(i) along the shoreline
(ii) perpendicular to the shoreline.
View SolutionA man rides a jet boat with a speed of 40km/hr in the north -east direction and the shore line makes an angle of 10∘ south of east . Find the component of the velocity of the jet boat
(i) along the shoreline and
(ii) perpendicular to the shoreline .
View Solution
Knowledge Check
A man rows a boat with a speed of 18 km/hr in northwest direction. The shoeline makes an angle of 15∘ south of west. Obtain the component of the velocity of the boat along the shoreline:
A9 km/hrB18√32 km/hrC18cos15∘ km/hrD18cos75∘ km/hrA boat which has a speed of 5 km h−1 in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. The velocity of the river water in km h−1 is
A1B3C4D√41
A man rows a boat with a speed 10 m/s along N-E direction. The shore line is 15∘ south of east. . What are components of the velocity vector along and perpendicular to shore?
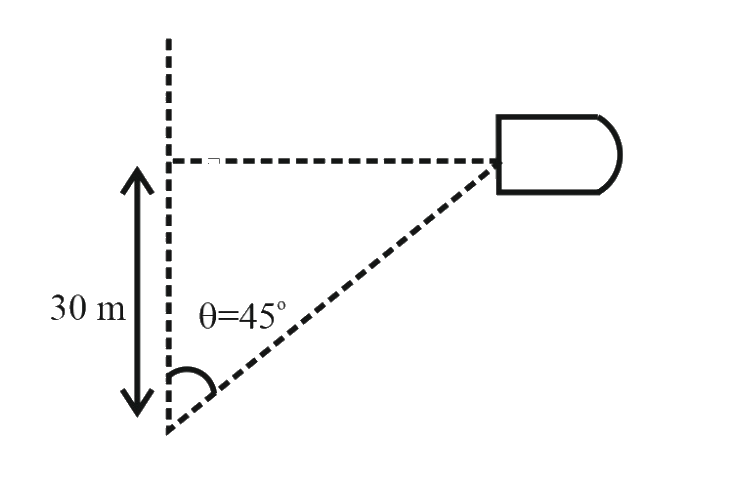
View SolutionA boat is travelling with a speed of 27 km h−1 due east. An observer is situated at 30 m south of the line of travel. The angular velocity of the boat relative to be the observer in the position shown will be
View SolutionA boat radioed a distress call to a Coast Guard station. At the time of the call, a vector A from the station to the boat had a magnitude of 45.0 km and was directed 15.0∘ east of north. A vector from the station to the point where the boat was later found is B=30.0km15.0∘ north of east.
What are the components of the vector from the point where the distress call was made to the point where the boat was found? In other words, what are the components of vector C=B−A?
View SolutionThe velocity of a body is 100kmh−1, 30^(@) west of south . Find the north ad east components of the vector.
View SolutionA motor boat is racing towards North at 25km/h and the water current in that region is 10km/h in the direction of 6000 East of South. Find the resultant velocity of the boat.
View SolutionA boat which has a spped of 5kmh−1 in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. Calculate the velocity of river water.
View Solution
