A man stands at the centre of a circular platform holding his arms extended horizontally with 4 kg block in each hand. He is set rotating about a vertical axis at 0.5rev/s. The moment of inertia of the man plus platform is 1.6kg−m2, assumed constant, the block are 90 cm from the axis of rotation. He now pulls the blocks in towards his body until they are 15 cm from the axis of rotation. Find (a) his new angular velocity and (b) the initial and final kinetic energy of the man and platform (c) how much work most the man do to pull int he blocks?
(a). I1ω1=I2ω2
∴ω2=I1I2ω1
=[1.6+(2)(4)(0.9)2][1.6+(2)(4)(0.15)2]×0.5
=(8.081.78)(0.5)
=2.27rev/s
=14.3rad/s
(b) Ki=12I1ω21
=12(1.6+(2)(4)(0.9)20.5×2π)2
=39.9J
Kf=12[1.6+(2)(4)(0.15)2](14.3)2
=181J
(c). W=Kf−Ki=141.1J
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A child of mass m is standing, on the periphery of a circular platform of radius R, which can rotate about its central axis. The moment of inertia of the platform is I. Child jumps off from the platform with a velocity u tangentially relative to the platform. Find the angular speed of the platform after the child jumps off.
View SolutionA turntable turns about a fixed vertical axis, making one revolution in 10s. The moment of inertia of the turntable about the axis is 1200kgm2. A man of 80kg, initially standing at centre of the turnable, runs out along the radius. What is the angular velocity of the turnable when the man is 2m from the centre?
View Solution
Knowledge Check
A ring of mass 10 kg and radius 0.2 m is rotating about its geometrical axis at 20 rev/sec. Its moment of inertia is
A0.2 kg - m2B3.0 kg - m2C0.4 kg - m2D5.0 kg - m2A body of moment of inertia about its axis of rotation is 3kgm2 and angular velocity 3 rad/s. The kinetic energy of rotating body is same as that of body of mass 27 kg moving with a speed of
A1.0 m/sB0.5 m/sC1.5 m/sD2.0 m/sTwo bodies of masses 1 kg and 2 kg, separated by 6 m are rotating about the centre of mass of the system. The moment of inertia of the system is
A12kgm2B24kgm2C36kgm2D6kgm2
A man stands on a rotating platform with his arms stretched holding a 5kg weight in each hand. The angular speed of the platform is 1.2revs−1. The moment of inertia of the man together with the platform may be taken to be constant and equal to 6kgm2. If the man brings his arms close to his chest with the distance n each weight from the axis changing from 100cm to20cm. The new angular speed of the platform is.
View SolutionA boy stands on a freely rotating platform with his arms extended. His rotation speed is 0.3 rev/s, when he draws in, his speed increases to 0.5 rev/s, then the ratio of his moment of inertia in these two cases will be
View SolutionA student sits on a freely rotating stool holding dumbbells, each of mass 5.0kg (Fig). When his arms are extended horizontally (Fig a), the dumbbells are 1.0m from the axis of rotation and the student rotate with an angular speed of 1.0rad/s. The moment of inertia of the student plus stool is 5.0kg.m2 and is assumed to be constant. The student pulls the dumbbells inward horizontally to a position 0.50m from the rotationa are (Fig.) The new angular speed of the student is.
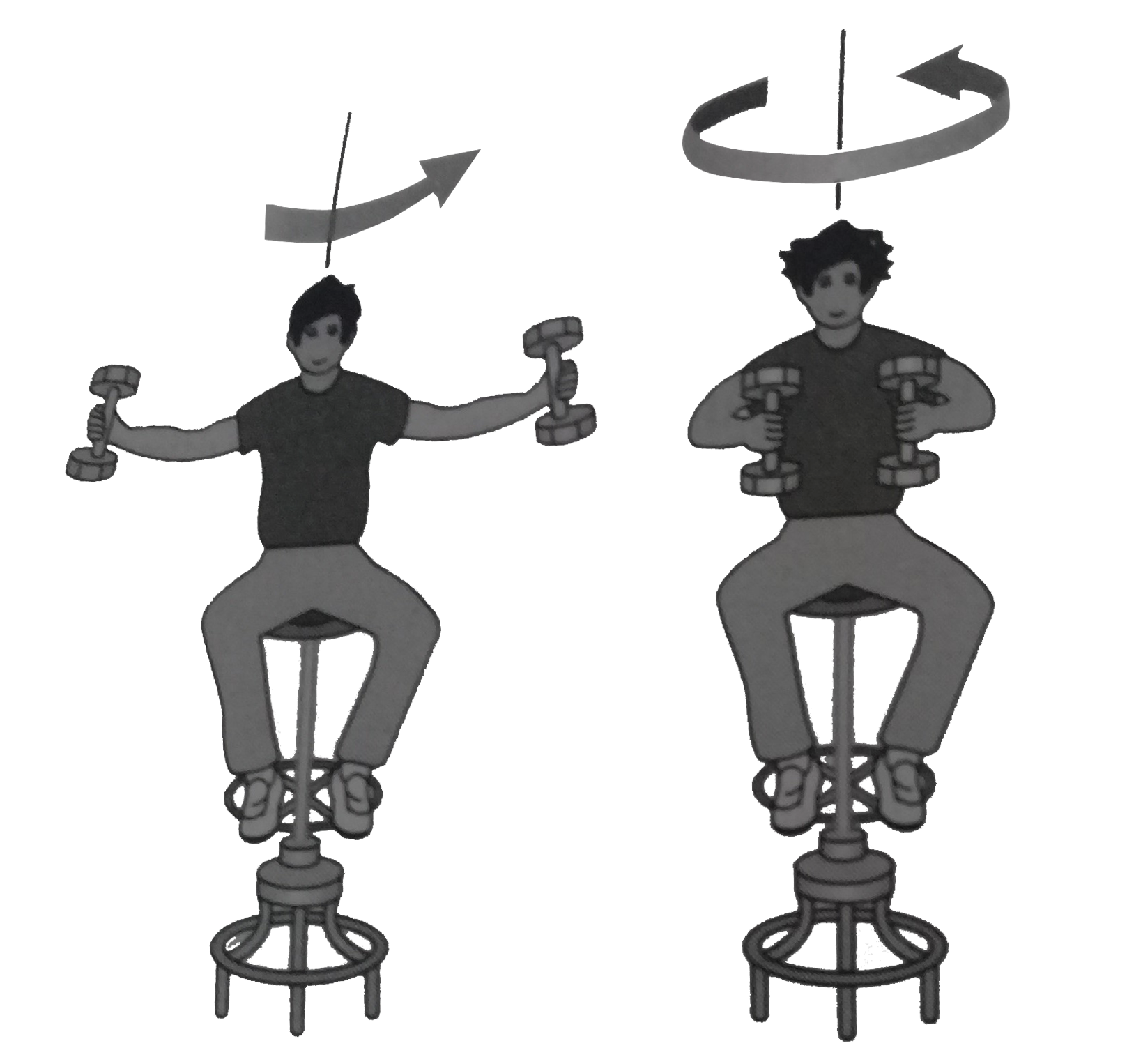 .
.
View SolutionA stone of mass 4kg is whirled in a horizontal circle of radius 1m and makes 2 rev/sec. The moment of inertia of the stone about the axis of rotation is
View SolutionThe rotational kinetic energy of a rigid body of moment of inertia 5 kg−m2 is 10 joules. The angular momentum about the axis of rotation would be -
View Solution
