A man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
.
10∘ upstream
20∘ upstream
30∘ upstream
60∘ upstream
The correct Answer is:D
(d) Refer to (Fig. S5.68) (a),
tanθ=vwvm=50100=12orvm=2vw
Refer to (Fig .S5.68) (b),
sin∝=vwvm=vw2vw=12
or θ=30∘
So, it is 60∘ upstream.
(a) 
,
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A swimmer can swim with speed 12 m/s in still water. Speed of river is 6 m/s. Find angle at which he should swim with downstream so that he reaches directly opposite point on other side
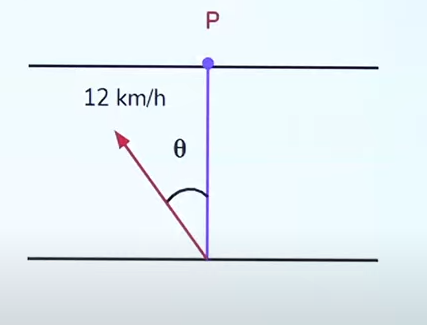View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View Solution
Knowledge Check
- Question 1 - Select One
A man is boat intends to cross river from A. If he rows perpendicular to the banks then he takes t1 = 10 minutes to reach the other bank and he reaches point C at a distance l = 120 m down the stream from the point B which is exactly opposite to A on the other bank. If he heads at a certain angle α to the straight path AB against the current he will reach point B in t2 = 12.5 minutes.
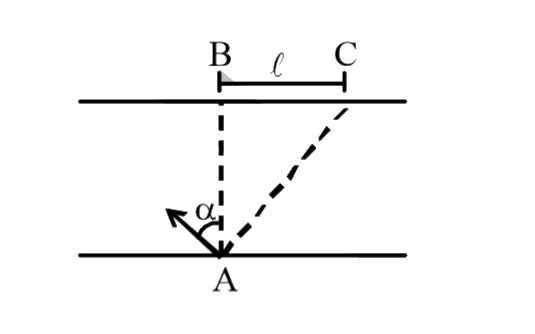
The width of river is-A180 mB200mC220 mDnone of these - Question 2 - Select One
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
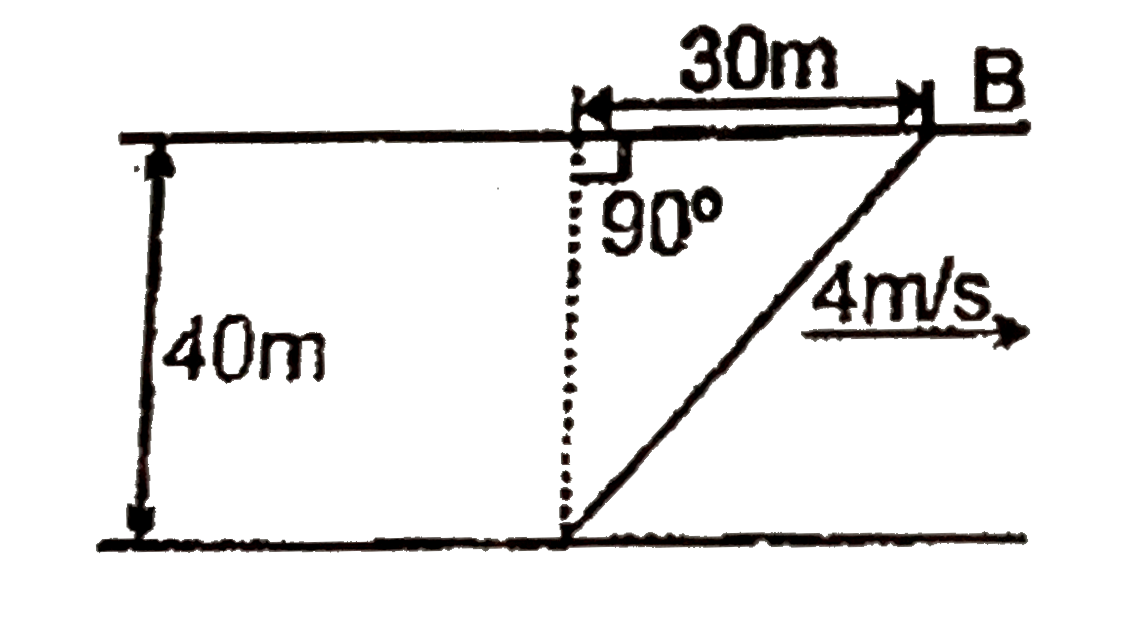A8m/sB3.2m/sC6.5m/sD7√2m/s
A man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View SolutionA swimmer wishes to reach directly opposite point on the other bank of a river,flowing with velocity 4√2ms.The swimmer can swim with 8ms in still water.The angle with the flow direction he should swim to reach the directly opposite point is (A)450 (B)900 (C)1350 (D)1500
View SolutionThe speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed u as shown in (Fig. 5.193). What minimum speed relative to water to water should the man have so that he can reach directly to point B ? In which direction should he swim ?
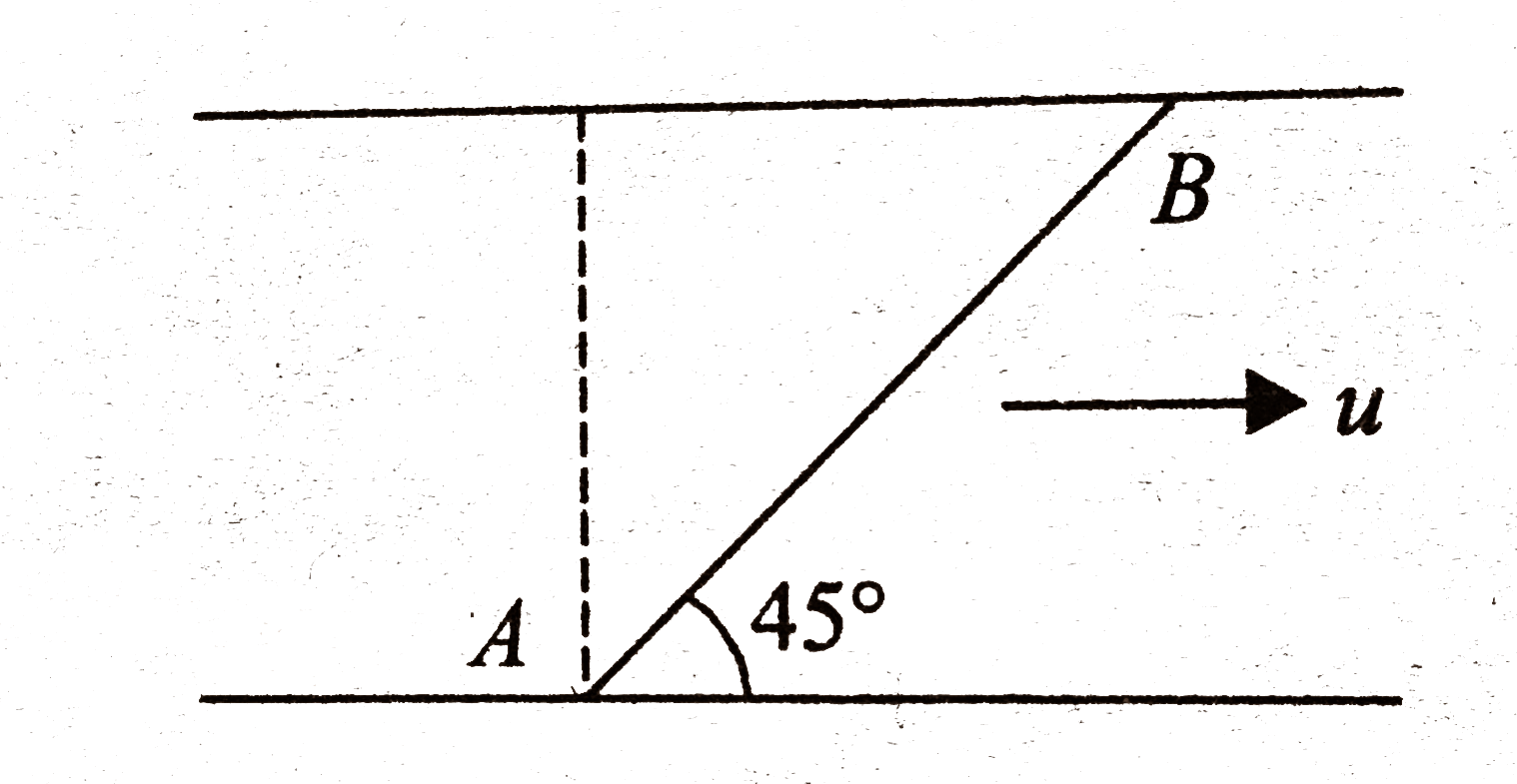.View SolutionGiven |Vbr|=4m/s= magnitude of velocity of boatman with respect to river, vr=2m/s in the directior shown. Boatman wants to reach from point A to point B. At what angle θ should he row his boat ?
View SolutionA man standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60o . When he retires 36 m from the bank, he finds the angle to be 30o . Find the breadth of the river.
View Solution