A man walk 20 m at an angle60∘ north of east . How far towards east has he he travellled ?
10 m
20 m
20√3 m
10√3m
The correct Answer is:A
To solve the problem of how far the man has traveled towards the east after walking 20 meters at an angle of 60 degrees north of east, we can break down the movement into its components using trigonometry.
1. Understand the Vector Components:
- The man walks at an angle of 60 degrees north of east. This means that we can break his movement into two components: one towards the east and one towards the north.
2. Identify the Magnitude of the Vector:
- The total distance walked by the man is given as 20 meters. This is the magnitude of the vector.
3. Determine the Eastward Component:
- To find out how far he has traveled towards the east, we need to calculate the eastward component of the vector. This can be done using the cosine of the angle.
- The formula for the eastward component (A_E) is:
AE=A⋅cos(θ)
- Where:
- A is the magnitude of the vector (20 meters).
- θ is the angle (60 degrees).
4. Calculate the Cosine of the Angle:
- We know that:
cos(60∘)=12
5. Plug in the Values:
- Now we can substitute the values into the formula:
AE=20⋅cos(60∘)=20⋅12=10 meters
6. Conclusion:
- Therefore, the man has traveled 10 meters towards the east.
Final Answer:
The distance traveled towards the east is 10 meters.
---
- The man walks at an angle of 60 degrees north of east. This means that we can break his movement into two components: one towards the east and one towards the north.
- The total distance walked by the man is given as 20 meters. This is the magnitude of the vector.
- To find out how far he has traveled towards the east, we need to calculate the eastward component of the vector. This can be done using the cosine of the angle.
- The formula for the eastward component (A_E) is:
AE=A⋅cos(θ)
- Where:
- A is the magnitude of the vector (20 meters).
- θ is the angle (60 degrees).
- We know that:
cos(60∘)=12
- Now we can substitute the values into the formula:
AE=20⋅cos(60∘)=20⋅12=10 meters
- Therefore, the man has traveled 10 meters towards the east.
The distance traveled towards the east is 10 meters.
Topper's Solved these Questions
Similar Questions
A car travles 6km towards north at an angle of 45∘ to the east and then travles distance of 4km towards north at an angle of 135∘ to east (figure). How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?
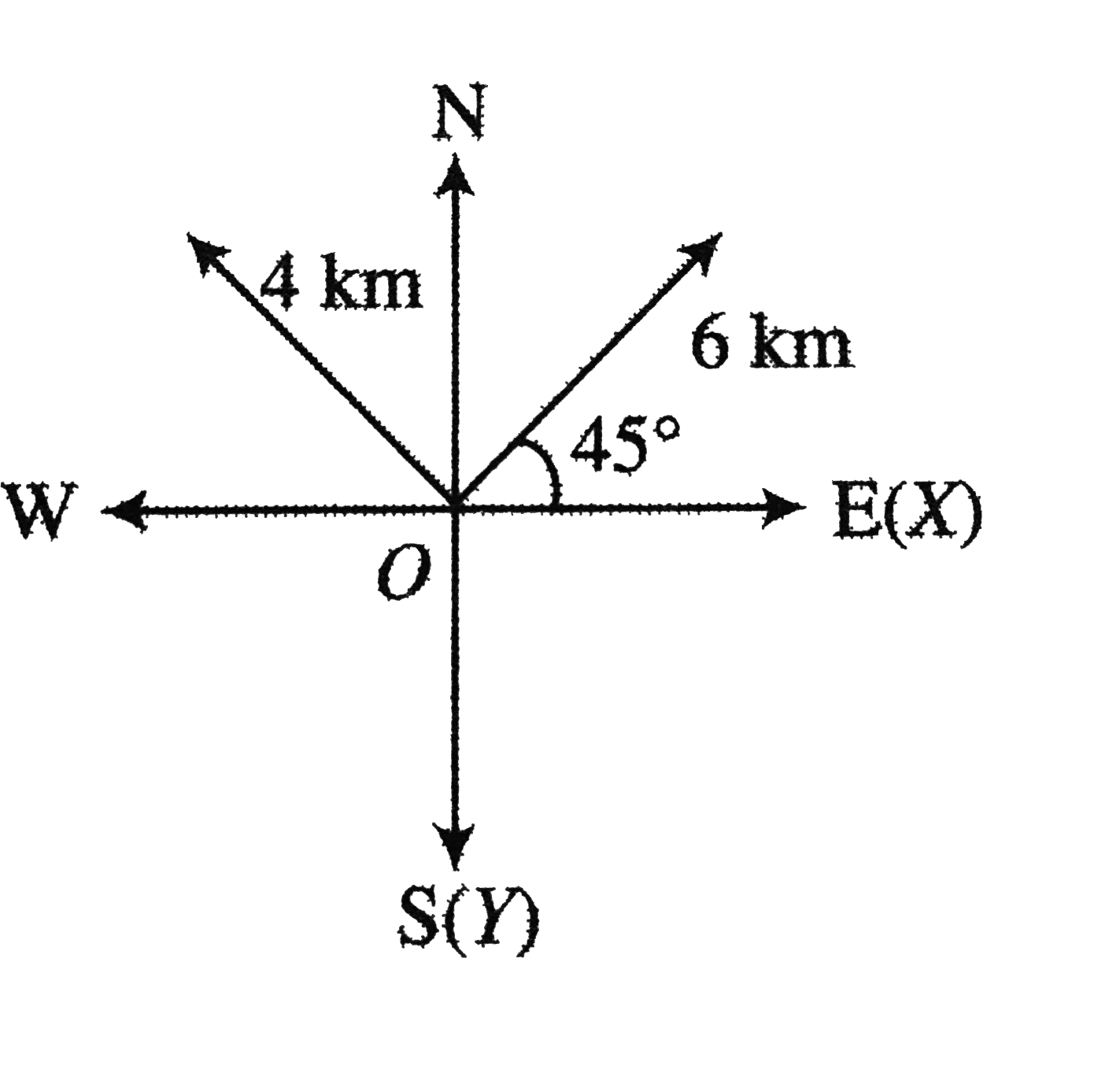
View SolutionA car travles 6km towards north at an angle of 45∘ to the east and then travles distance of 4km towards north at an angle of 135∘ to east (figure). How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?

View Solution
Knowledge Check
A man walks 4 km towards the north in one hour and then 3 km towards the east in the next hour. His average velocity is
A3.5kmh−1B2.5kmh−1C5kmh−1D6kmh−1
A flag leaning to wards the east is inclined at an angle θ to the ground. A man walks a distance of 4 m from the foot of the flag towards the west and the observes the angle of elevation of the top of the flag to be 45∘. If, on walking a further distance of 3 m in the same direction, the angle of elevation decreases by 15∘,tanθ is equal to
View SolutionA man walks 2 km dur north .After that he walks another 2 km along
due east
View SolutionA body A is standing 20√3 m away in a direction 30∘ north of east from east. In a Cartesian coordinate system with its x-axis towards the east, the position of C with respect to A is
View SolutionIt is raining at a speed of 5ms−1 at an angle 37∘ to vertical, towards east. A man is moving to west with a velocity of 5ms−1. The angle with the vertical at which he has to hold the umbrella to protect himself from rain is
View SolutionA source is moving with constant speed υs=20m/s towards a stationary observer due east of the source. Wind is blowing at the speed of 20m/s at 60∘ north of east. The source has frequency 500HZ. Speed of sound =300m/s. The frequency resgistered by the observer is approximately
View SolutionA man starts from his home and walks 50 m towards, then he turns towards east and walks 40 m and then reaches to his office after moving 20 m towards south.
(i) What is the total distance covered by the man from his home to office ?
(ii) What is his displacement from his home to office ?
View SolutionA block is applied two forces of magnitude 5N each. One force is acting towards East and the other acting along 60∘ North of East. The resultant of the two forces (in N) is of magnitude :-
View Solution
