A block is applied two forces of magnitude 5N each. One force is acting towards East and the other acting along 60∘ North of East. The resultant of the two forces (in N) is of magnitude :-
The correct Answer is:√75
To find the resultant of the two forces acting on the block, we can follow these steps:
Step 1: Identify the Forces
We have two forces:
- F1=5N acting towards the East.
- F2=5N acting at an angle of 60∘ North of East.
Step 2: Draw a Diagram
Draw a coordinate system with East as the positive x-axis and North as the positive y-axis.
- Draw F1 along the x-axis (East).
- Draw F2 at an angle of 60∘ from the x-axis (East) towards the y-axis (North).
Step 3: Resolve the Forces into Components
To find the resultant force, we need to resolve F2 into its x and y components:
- F2x=F2cos(60∘)=5cos(60∘)=5×12=2.5N
- F2y=F2sin(60∘)=5sin(60∘)=5×√32=5√32N
Step 4: Calculate the Resultant Components
Now, we can find the total components in the x and y directions:
- Total x-component, Rx=F1+F2x=5+2.5=7.5N
- Total y-component, Ry=F2y=5√32N
Step 5: Calculate the Magnitude of the Resultant Force
Using the Pythagorean theorem, the magnitude of the resultant force R can be calculated as:
R=√R2x+R2y
Substituting the values:
R=
⎷(7.5)2+(5√32)2
Calculating each term:
R=√56.25+754=√56.25+18.75=√75
Step 6: Final Result
Thus, the magnitude of the resultant force is:
R=√75N
We have two forces:
- F1=5N acting towards the East.
- F2=5N acting at an angle of 60∘ North of East.
Draw a coordinate system with East as the positive x-axis and North as the positive y-axis.
- Draw F1 along the x-axis (East).
- Draw F2 at an angle of 60∘ from the x-axis (East) towards the y-axis (North).
To find the resultant force, we need to resolve F2 into its x and y components:
- F2x=F2cos(60∘)=5cos(60∘)=5×12=2.5N
- F2y=F2sin(60∘)=5sin(60∘)=5×√32=5√32N
Now, we can find the total components in the x and y directions:
- Total x-component, Rx=F1+F2x=5+2.5=7.5N
- Total y-component, Ry=F2y=5√32N
Using the Pythagorean theorem, the magnitude of the resultant force R can be calculated as:
R=√R2x+R2y
Substituting the values:
R=
⎷(7.5)2+(5√32)2
Calculating each term:
R=√56.25+754=√56.25+18.75=√75
Thus, the magnitude of the resultant force is:
R=√75N
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)
7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Single Correct Type Questions.
34 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Solved Examples
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
Two forces of magnitudes 3N and 4 N act together on an object making an angle 60∘ with each other. Find the resultant force acting on the object.
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
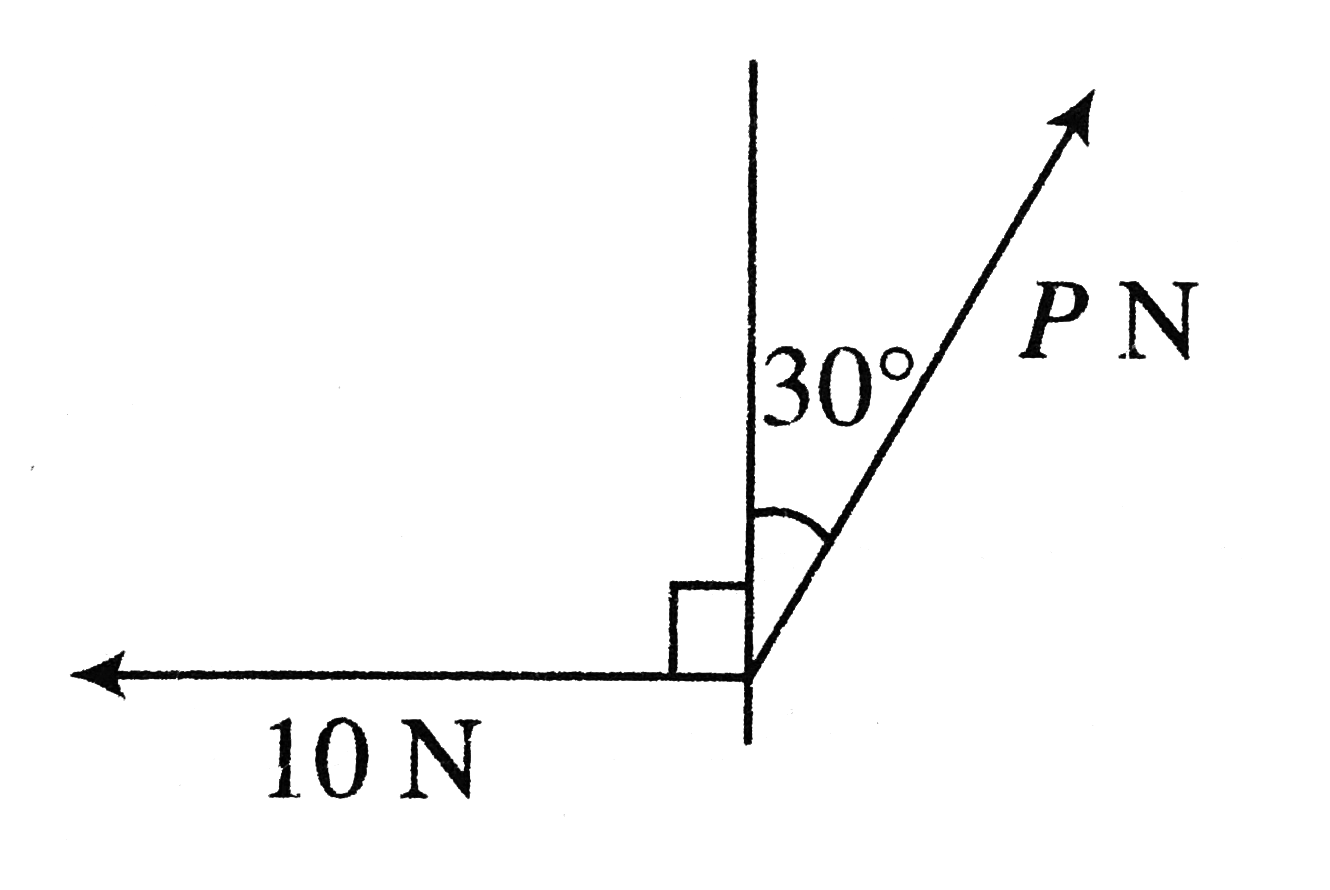
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
Two equal forces are acting at a point with an angle 60∘ between them. If the resultant force is equal to 4√3N, the magnitude of each force is
View SolutionThree forces of magnitudes 2N, 3N and 6N act at corners of a cube along three sides as shown in figure. Find the resultant of these forces in N.
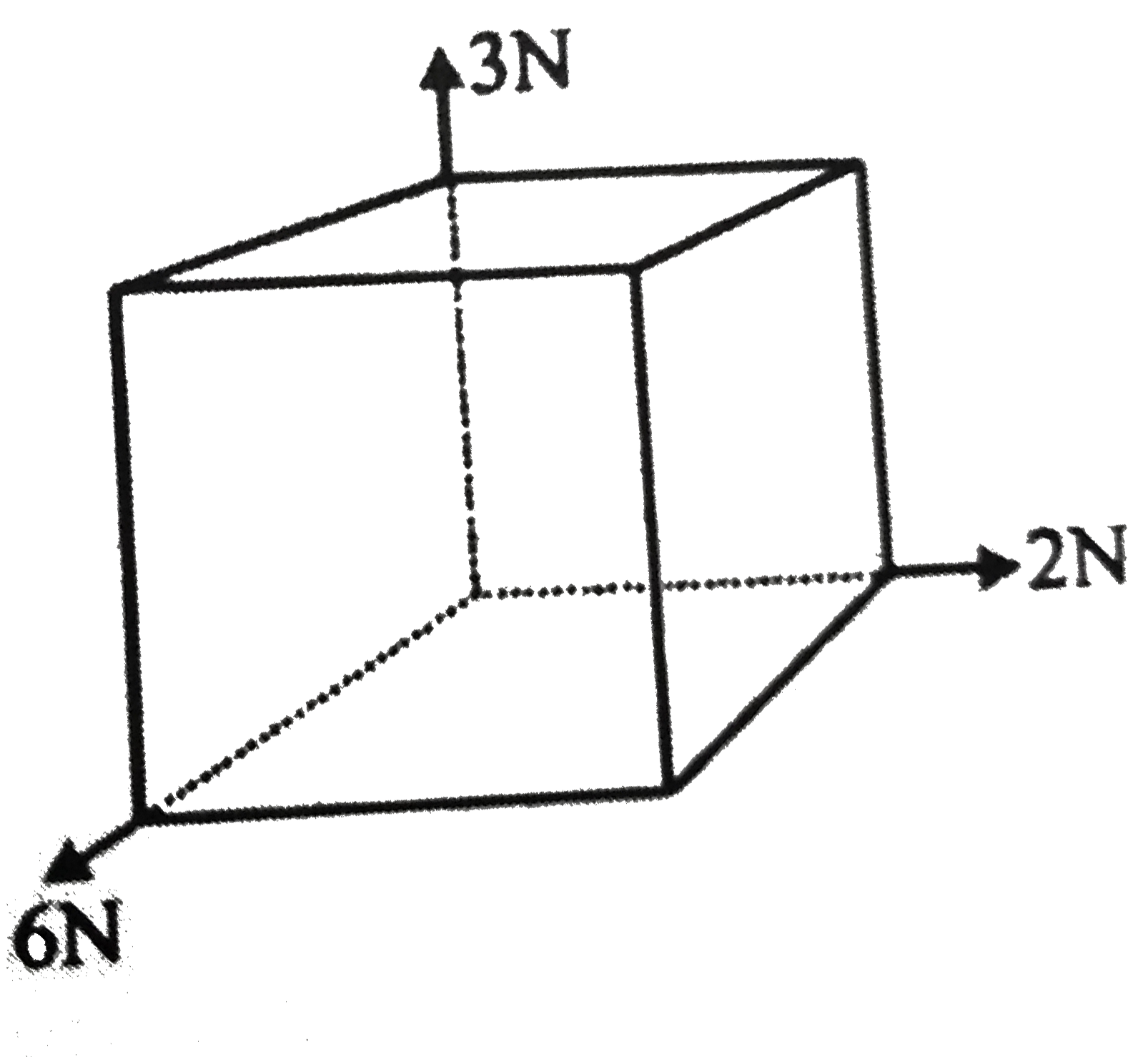
View SolutionTwo forces of magentude 7 newton and 5 newton act on a particle at an angle θ can have any value . The minimum magnitude of the resultant forces is :
View SolutionThe resultant of two forces at right angles is 13N. The minimum resultant of the two forces is 7 N. The forces are
View SolutionTwo equal forces are acting at a point with an angle of 60∘ between them. If the resultant force is equal to 40√3N, The magnitude of each force is :-
View SolutionTwo perpendicular forces of magnitudes 10 N and 5 N act at a point. Find their resultant.
View SolutionThe resultant of two forces has magnitude 20N. One of the forces is of magnitude 20√3N and makes an angle of 30∘ with the resultant. Then what is the magnitude of the other force?
View Solution
