A man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
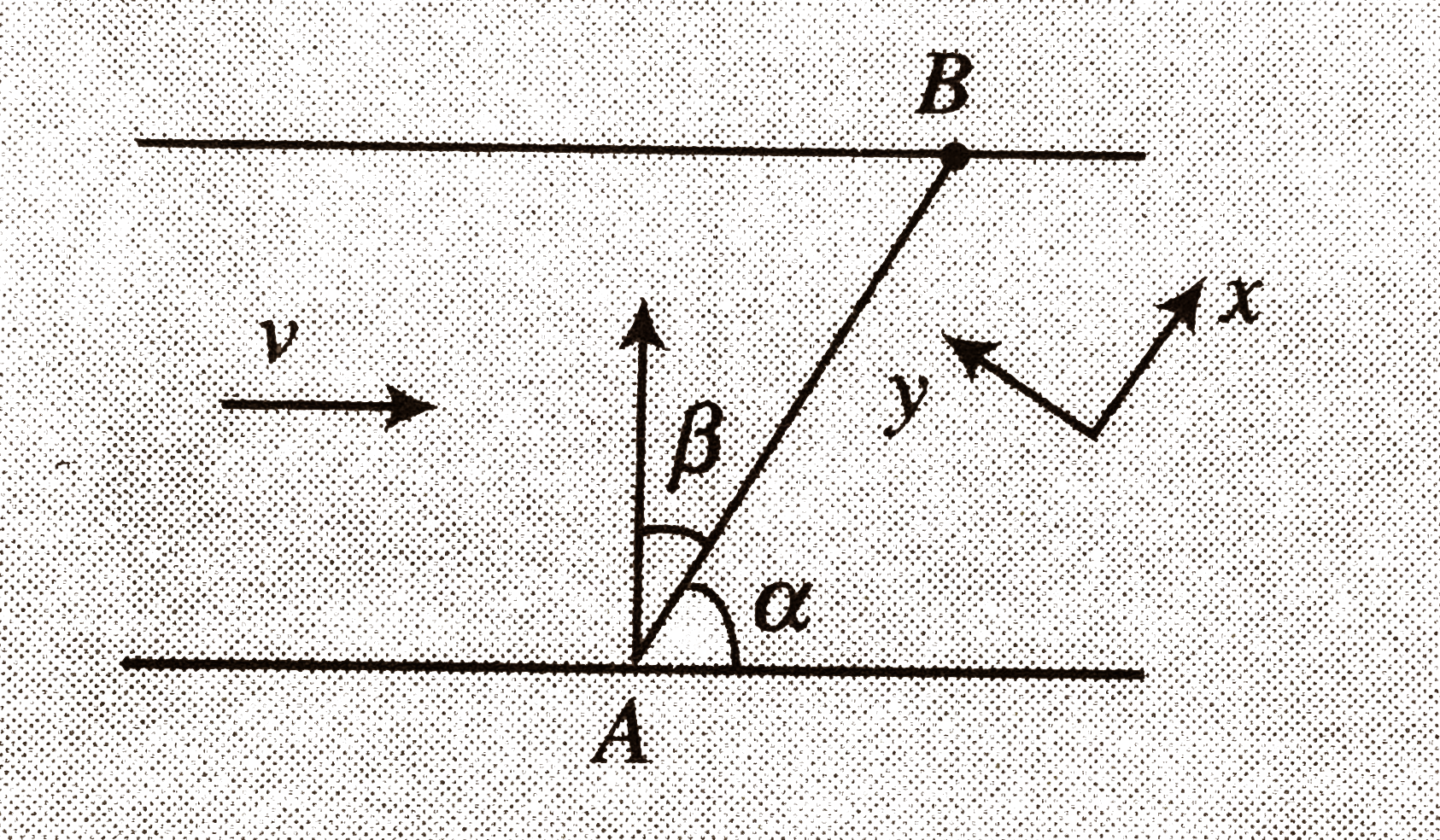 .
.
In this problem, we choose axis along AB and normal to is it.
Since the man moves along AB, the velocity components of current and man normal to AB must cancel out, i.e.,
usinβ=vsin∝
When the man moves from A to B, his resultant velocity along AB=(ucosβ+vcos∝)
Hence, S=(ucosβ+vcos∝)t1
while for motion from B to AS=(ucosβ−vcos∝)t2
From the condition of the problem, t1+t2=t
Sucosβ+vcos∝+Sucosβ−vcos∝=t
s[ucosβ−vcos∝+ucosβ+vcos∝u2cos2β−v2cos2∝]=t
S(2ucosβ)u2cos2β−v2cos2∝=t.
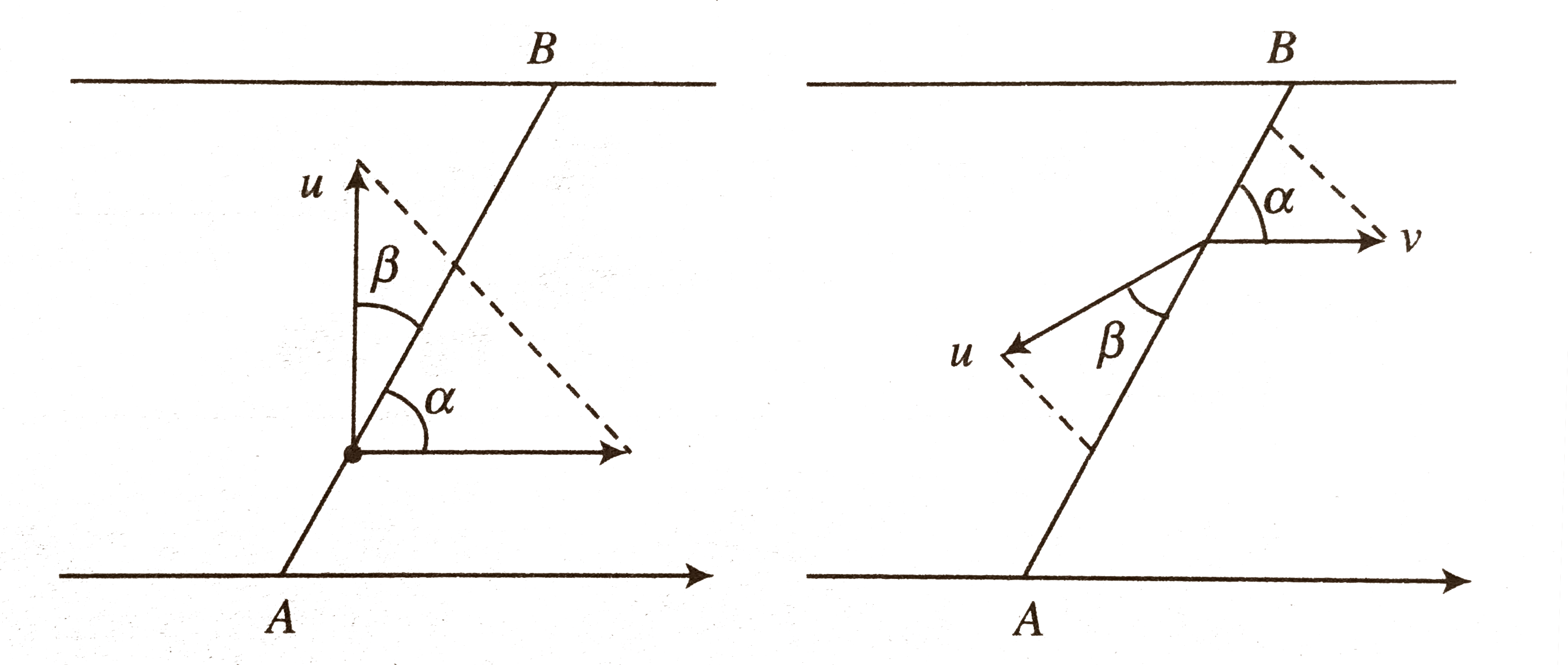 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current v=1.9m/s is constant over the entire width of the river. The line AB makes an angle α=60∘ with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time t=5min? The angle beta remains the same during the passage from A to B and from B to A.
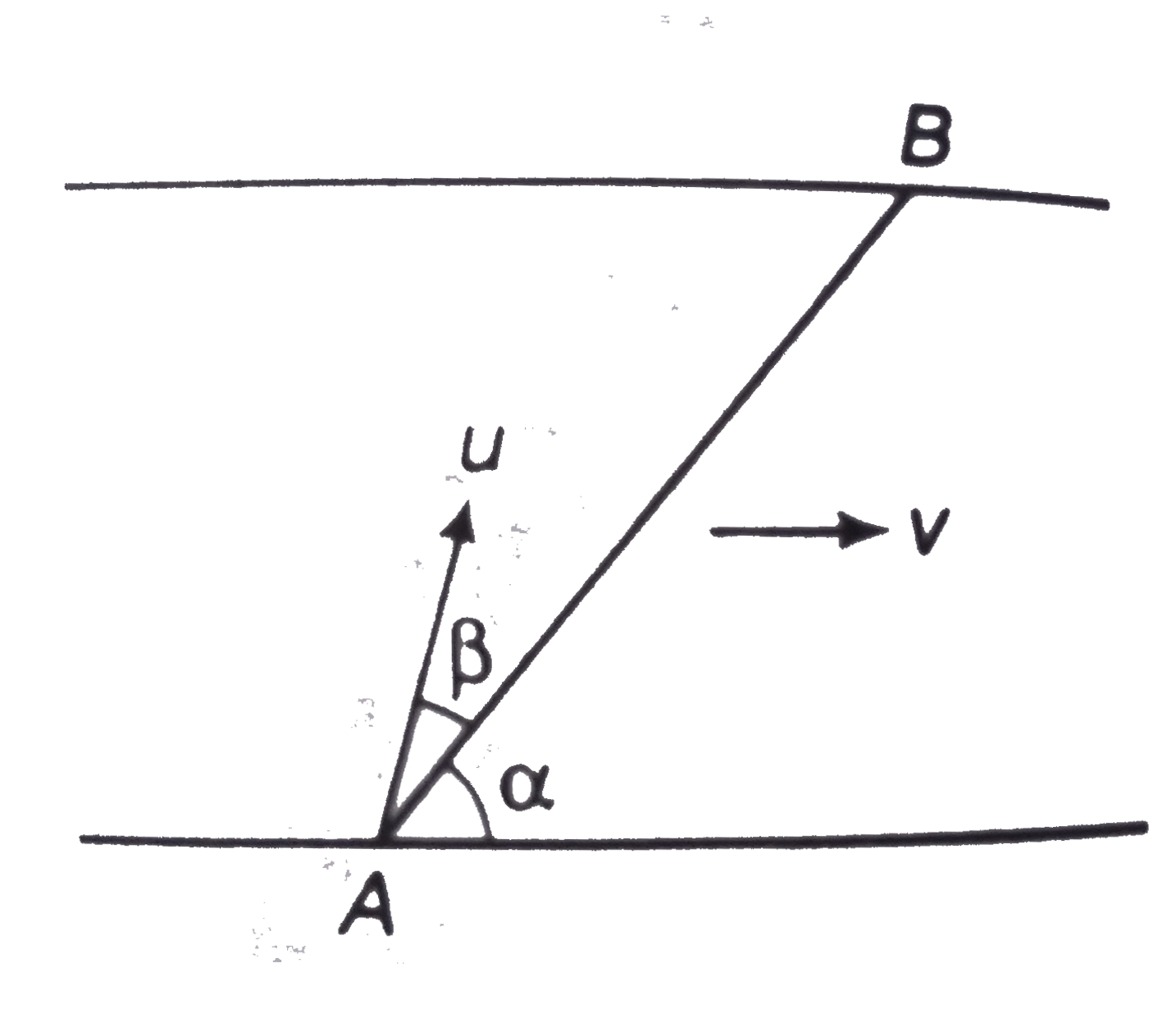
View SolutionA steamer plies between two stations AandB on opposite banks of a river, always following the path AB. The distance between stations AandB is 1200m. The velocity of the current is √17ms−1 and is constant over the entire width of the river. The line AB makes an angle 60∘ with the direction of the flow. The steamer takes 5min to cover the distance AB and back.
(a) Find the velocity of steamer with respect to water.
(b) In what direction should the steamer move with respect to line AB ?
View Solution
Knowledge Check
A man wishes to cross a river flowing with velocity u swims at an angle θ with the river flow.If the man swims with speed vand if the width of the river is d, then the drift travelled by him is
A(u+vcosθ)dvsinθB(u−vcosθ)dvsinθC(u−vcosθ)dvcosθD(u+vcosθ)dvcosθA swimmer crosses the river along the line making an angle of 45∘ with the direction of flow. Velocity of the river is 5 m/s. Swimmer takes 6 seconds to cross the river of width 60 m. The velocity of the swimmer with respect to water will be :
A10m/sB12m/sC5√5m/sD10√2m/sA man wishes to cross a river to an exactly opposite point on the other bank. if the can swim with twice the velocity of the current, the inclination to the current of the direction he should swim is
A30∘B45∘C60∘D120∘
A steamer plies between two stations AandB on opposite banks of a river, always following the path AB. The distance between stations AandB is 1200m. The velocity of the current is √17ms−1 and is constant over the entire width of the river. The line AB makes an angle 60∘ with the direction of the flow. The steamer takes 5min to cover the distance AB and back.
(a) Find the velocity of steamer with respect to water.
(b) In what direction should the steamer move with respect to line AB ?
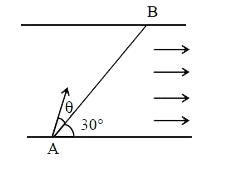
View SolutionA swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30∘ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be _________ ∘, so that the swimmer reaches point B.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA man directly crosses a river in time t1 and swims down the current a distance equal to the width of the river I time t2. If uandv be the speed of the current and the man respectively, show that : t1:t2=√v+u:√v−u).
View Solution
