A man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
(a)The minimum time in which he can cross the river is bv
(b)He can reach a point exactly opposite on the bank in time t=b√v2−u2ifv>u
(c)He cannot reach a point exactly opposite on the bank if u>v
(d)He cannot reach a point exactly opposite on the bank if v>u
The correct Answer is:A, B, C
To solve the problem of a man swimming across a river with a current, we need to analyze the situation step by step.
Step 1: Understand the Problem
We have a river of width b flowing with a speed u. The man can swim at a velocity v relative to the water. We need to determine the time it takes for him to cross the river and whether he can reach a point directly opposite on the other bank.
Step 2: Set Up the Diagram
1. Draw a diagram of the river. Label the width of the river as b.
2. Represent the man's swimming direction at an angle θ to the bank.
3. The river flows downstream with velocity u.
Step 3: Determine the Resultant Velocity
The man's swimming velocity can be broken down into two components:
- The component perpendicular to the river (across the width) is vcos(θ).
- The component parallel to the river (downstream) is vsin(θ).
The resultant velocity Vn of the man relative to the ground can be calculated using the Pythagorean theorem:
Vn=√(vcos(θ))2+(u+vsin(θ))2
Step 4: Calculate the Time to Cross the River
The time t taken to cross the river is given by the width of the river divided by the component of the man's velocity that is directed across the river:
t=bvcos(θ)
Step 5: Conditions for Reaching Directly Opposite
To reach a point directly opposite on the bank, the downstream drift caused by the river's current must be countered by the man's swimming. This can be expressed as:
u=vsin(θ)
If u>v, then sin(θ) would need to be greater than 1, which is impossible. Thus, if u>v, he cannot reach the point directly opposite.
Step 6: Analyze the Options
1. Minimum Time: The minimum time occurs when there is no current (i.e., u=0). Thus, the minimum time is:
tmin=bv
This option is correct.
2. Time to Reach Opposite Bank: If v>u, the time to reach a point directly opposite is:
t=b√v2−u2
This option is also correct.
3. Cannot Reach Opposite Point: If u>v, he cannot reach the opposite point, which is correct.
4. Incorrect Statement: The statement that he cannot reach a point directly opposite if v>u is incorrect, as he can reach the opposite bank.
Conclusion
The correct statements are:
- Minimum time to cross the river is bv.
- He can reach a point directly opposite in time t=b√v2−u2 if v>u.
- He cannot reach a point directly opposite if u>v.
Final Answer
The correct options are A, B, and C.
---
We have a river of width b flowing with a speed u. The man can swim at a velocity v relative to the water. We need to determine the time it takes for him to cross the river and whether he can reach a point directly opposite on the other bank.
1. Draw a diagram of the river. Label the width of the river as b.
2. Represent the man's swimming direction at an angle θ to the bank.
3. The river flows downstream with velocity u.
The man's swimming velocity can be broken down into two components:
- The component perpendicular to the river (across the width) is vcos(θ).
- The component parallel to the river (downstream) is vsin(θ).
Vn=√(vcos(θ))2+(u+vsin(θ))2
The time t taken to cross the river is given by the width of the river divided by the component of the man's velocity that is directed across the river:
t=bvcos(θ)
To reach a point directly opposite on the bank, the downstream drift caused by the river's current must be countered by the man's swimming. This can be expressed as:
u=vsin(θ)
If u>v, then sin(θ) would need to be greater than 1, which is impossible. Thus, if u>v, he cannot reach the point directly opposite.
1. Minimum Time: The minimum time occurs when there is no current (i.e., u=0). Thus, the minimum time is:
tmin=bv
This option is correct.
t=b√v2−u2
This option is also correct.
The correct statements are:
- Minimum time to cross the river is bv.
- He can reach a point directly opposite in time t=b√v2−u2 if v>u.
- He cannot reach a point directly opposite if u>v.
The correct options are A, B, and C.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective Questions
24 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A man can swim at a speed of 5 km/h W.r.t water. He wants to cross a 1.5 km wide river flowing at 3 km/h. He keeps himself always at an angle of 60° with the flow of direction while swimming, The time taken by him to cross the river will be
View SolutionA man can swim at a speed of 3 km/h in still water. He wants t cross a 500 m wide river flowing at 2 km/h. He flow at an angle of 120 with the river flow while swimming. A. Find the time he takes to cross the river. b.At what point on the opposite bank will he arrive?
View SolutionA man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The time taken to cross the river is.
View SolutionA man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The drift of the man along the direction of flow, when he arrives at the opposite bank is.
View SolutionA man can swim in still water with a speed of 2ms−1. If he wants to cross a river of water current speed √3ms−1 along the shortest possible path, then in which direction should he swim ?
View SolutionA man can swim in still water ast a speed of 3 km/h. He wants to cross a river that flows at 2 km/h and reach the point directly oposite to his starting point. A. In which diretionshoeld he try to swim (that is, find the angle his body makes wilth the river flow)? b. How much time will he take to cross the river if the river is 500 m wide?
View SolutionA man can swin with speed 6 km/h in still water. If he tries of swim across a river flowing with speed 5km/h, how fast does a leaf floating on water appears to go , to the man ?
View SolutionA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
The time take by boat to cross the river is
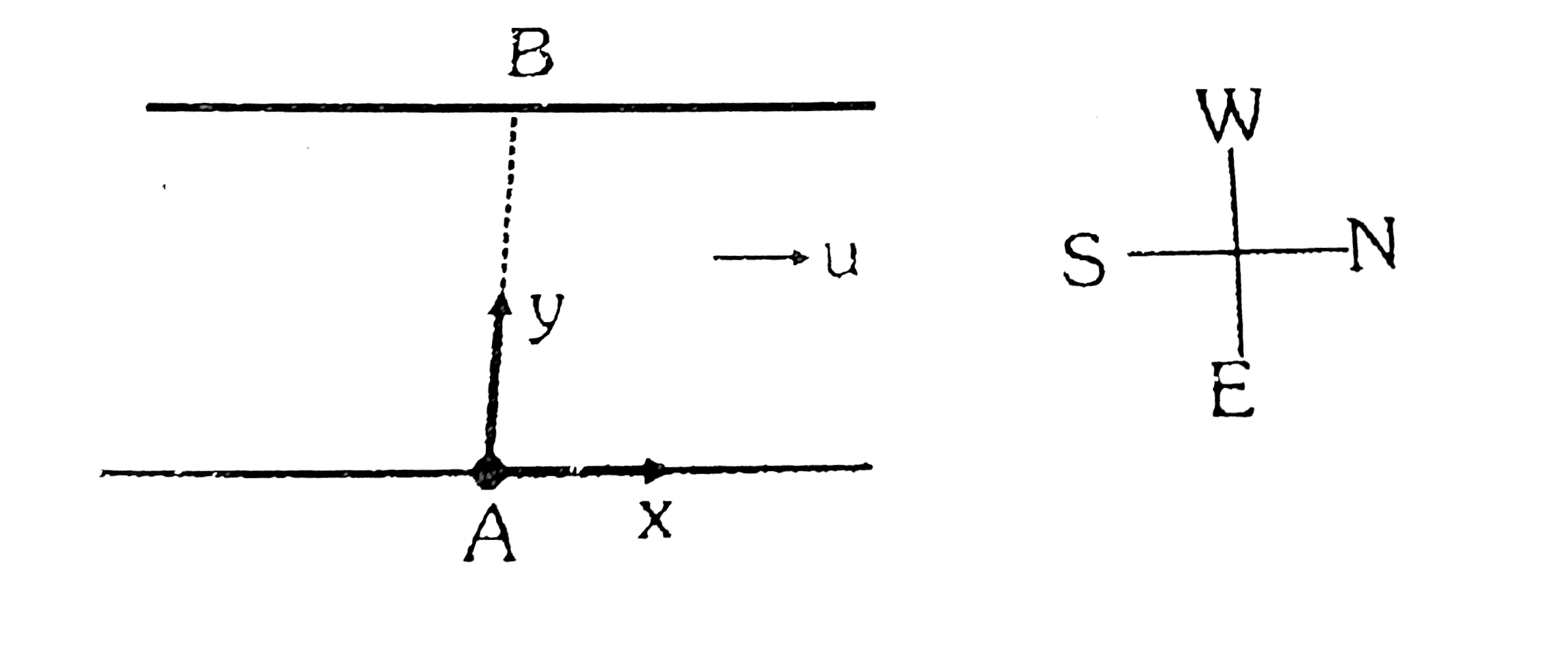
View SolutionA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
The time take by boat to cross the river is
View SolutionA river of width a with straight parallel banks flows due north with speed u. The points O and A are on opposite banks and A is due east of O. Coordinate axes Ox and Oy are taken in the east and north directions respectively. A boat, whose speed is v relative to water, starts from O and crosses the river. If the boat is steered due east and u varies with xas:u=x(a−x)va2. Find
(a) equation of trajectory of the boat,
(b) time taken to cross the river,
(c) absolute velocity of boatman when he reaches the opposite bank,
(d) the displacement of boatman when he reaches the opposite bank from the initial position.
View Solution
