A mass 2 kg describes a circle of radius 1 m on a smooth horizontal table at a uniform speed .If is joined to the centre of the circle by a string, which can just withstand 32 N, then the greatest number of revolution per minute , perfomed by the mass would be
38
4
76
16
The correct Answer is:A
To find the greatest number of revolutions per minute that a mass can perform while being attached to a string that can withstand a maximum tension of 32 N, we can follow these steps:
1. Identify the Given Values:
- Mass (m) = 2 kg
- Radius (r) = 1 m
- Maximum Tension (T) = 32 N
2. Understand the Relationship between Tension and Centripetal Force:
- The tension in the string provides the centripetal force required for circular motion.
- The formula for centripetal force (F_c) is given by:
Fc=mω2r
- Here, ω is the angular velocity in radians per second.
3. Set Up the Equation:
- Since the maximum tension the string can withstand is 32 N, we can set up the equation:
T=mω2r
- Substituting the known values:
32=2⋅ω2⋅1
4. Solve for Angular Velocity (ω):
- Rearranging the equation gives:
ω2=322=16
- Taking the square root:
ω=√16=4 rad/s
5. Convert Angular Velocity to Revolutions per Minute (RPM):
- To convert from radians per second to revolutions per minute, use the conversion factor:
RPM=ω⋅602π
- Substituting the value of ω:
RPM=4⋅602π=2402π=120π
6. Calculate the Final Value:
- Using π≈3.14:
RPM≈1203.14≈38.19
7. Final Answer:
- The greatest number of revolutions per minute performed by the mass is approximately 38.19 RPM. The closest answer is 38 RPM.
- Mass (m) = 2 kg
- Radius (r) = 1 m
- Maximum Tension (T) = 32 N
- The tension in the string provides the centripetal force required for circular motion.
- The formula for centripetal force (F_c) is given by:
Fc=mω2r
- Here, ω is the angular velocity in radians per second.
- Since the maximum tension the string can withstand is 32 N, we can set up the equation:
T=mω2r
- Substituting the known values:
32=2⋅ω2⋅1
- Rearranging the equation gives:
ω2=322=16
- Taking the square root:
ω=√16=4 rad/s
- To convert from radians per second to revolutions per minute, use the conversion factor:
RPM=ω⋅602π
- Substituting the value of ω:
RPM=4⋅602π=2402π=120π
- Using π≈3.14:
RPM≈1203.14≈38.19
- The greatest number of revolutions per minute performed by the mass is approximately 38.19 RPM. The closest answer is 38 RPM.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
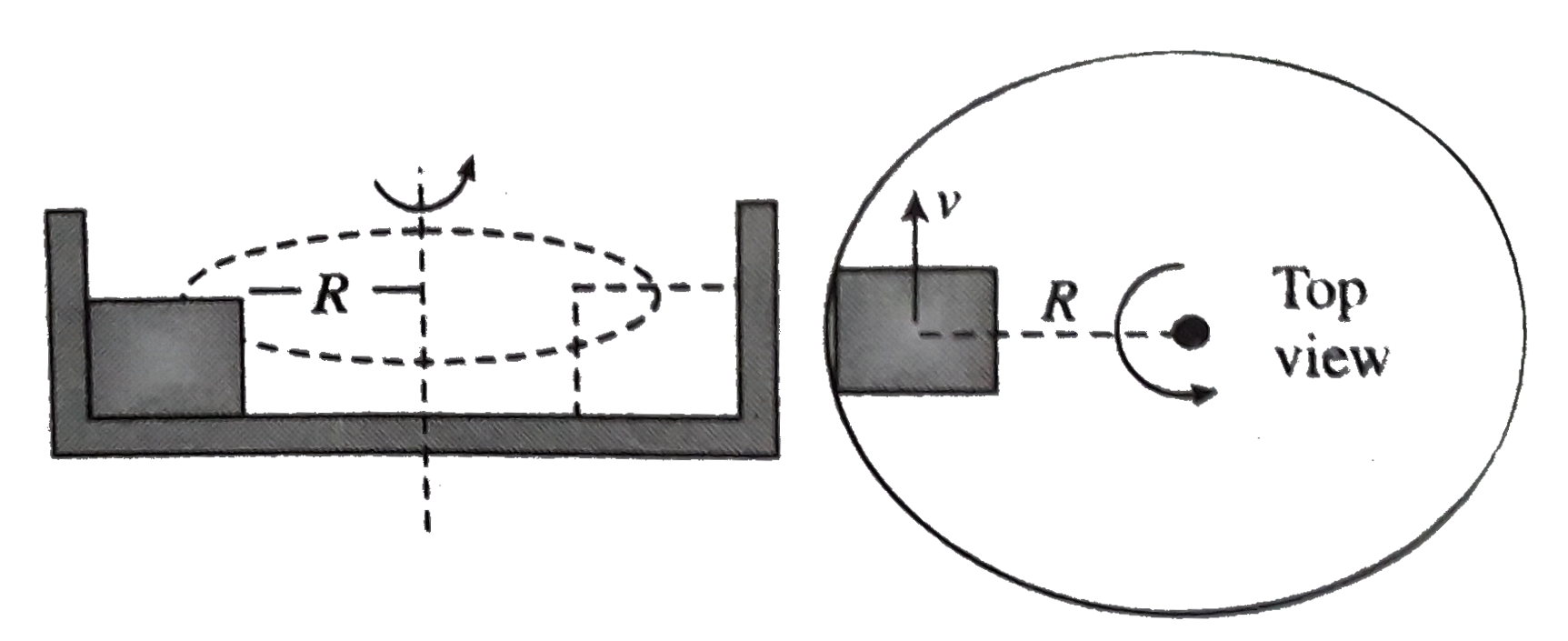 Amv2RBmgCm√v4R2+4g2Dm√v4R2+g2
Amv2RBmgCm√v4R2+4g2Dm√v4R2+g2A particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point , its
AKinetic energy changes by MV2/4Bmomentum does not changeCMomentum changes by 2MVDkinetic energy changes by MV2A particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point, its
AKinetic energy changes by MV2/4BMomentum does not changeCMomentum changes by 2 MVDKinetic energy changes by MV2
A point mass of 2 kg tied to a string of 1 m length is rotated in a vertical circle with uniform speed of 4m/s. The tension in the string is nearly 32 N when mass is at
View SolutionA particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
View SolutionA particle of mass 1 kg is revolved in a horizontal circle of radius 1 m with the help of a string. IF the maximum tension the string can with stand is 16π2 N, then the maximum frequency with which the particle can revolve is
View SolutionA mass of 5 kg is tied to a string of length 1.0 m and is rotated in vertical circle with a uniform speed of 4m/s . The tension in the string will be 130 N when the mass is at (g= 10m/s2)
View SolutionA stone of mass 0.3kg attched to a 1.5m long stirng is whirled around in a horizontal cirlcle at a speed of 6 m/s The tension in the string is
View Solution
