A particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
√5gr
√4gr/3
√3gr/2
√√3gr
The correct Answer is:C
Step by step video, text & image solution for A particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r//2 below the centre of the sphere. What is its speed ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Advance MCQs
Explore 17 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Conceptual MCQs
Explore 23 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
Similar Questions
A small block of mass m moving on inside of the smooth hemisphere of radius R, describes a horizontal circle at a distance R/2 below the centre of the sphere. Find the time period of revolution and force with which the block pushes against the hemisphere.
View SolutionParticle slides down the surface of a smooth fixed sphere of radius r starting from rest at the highest point. Find where it will leave the sphere. Show that it strike the horizontal plane through the lowest point of the sphere at a distance equal to 5[√5+4√2](r/27) from the vertical diameter.
View Solution
Knowledge Check
The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0RThe radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
ArB0.5 rC√0.6rD√0.4rA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
Amg2B3mg8Cmg16Dnone of these
A spherical cavity of radius R2 is made in a sphere of radius R and mass M. The centre of the cavity is at a distance R2 from the centre of the sphere. The intensity of gravitational field at the centre of cavity is GMnR2. Find n.
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
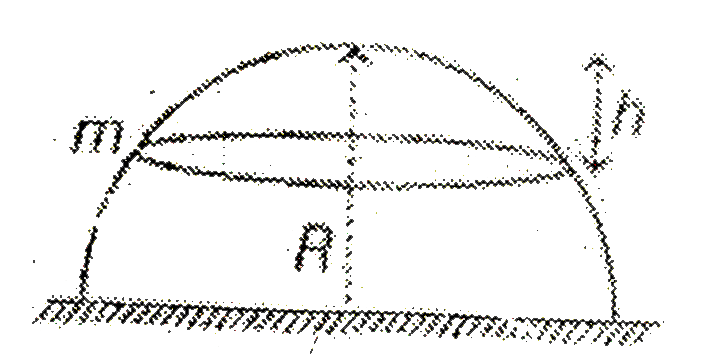
View SolutionA unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionLet ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
View Solution