"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
To solve the problem of what happens to the length of a spring when a mass is attached to one end and the spring is whirled in a horizontal circle, we can analyze the forces acting on the mass and the spring.
1. Understanding the System:
- We have a mass m attached to a spring with a spring constant k. The other end of the spring is held in hand, and the mass is rotated in a horizontal circle.
2. Identify Forces:
- The mass experiences a centripetal force that is required to keep it moving in a circular path. This centripetal force is provided by the spring force.
3. Centripetal Force Equation:
- The centripetal force Fc required to keep the mass moving in a circle of radius r is given by:
Fc=mω2r
where ω is the angular velocity and r is the radius of the circular path.
4. Spring Force Equation:
- The force exerted by the spring when it is stretched by an amount x from its natural length L is given by Hooke's Law:
Fs=kx
5. Relating the Forces:
- Since the spring provides the centripetal force, we can equate the two forces:
kx=mω2r
- Here, r is the total length of the spring when stretched, which can be expressed as:
r=L+x
6. Substituting for r:
- Substitute r into the centripetal force equation:
kx=mω2(L+x)
7. Rearranging the Equation:
- Rearranging gives:
kx=mω2L+mω2x
- This can be rearranged to:
kx−mω2x=mω2L
- Factoring out x:
x(k−mω2)=mω2L
8. Solving for x:
- Thus, we can solve for x:
x=mω2Lk−mω2
9. Analyzing the Result:
- The length of the spring when stretched is L+x. As ω increases, mω2 increases, which affects the denominator k−mω2. If mω2 approaches k, x will increase significantly, indicating that the spring stretches more.
10. Conclusion:
- As the mass is whirled in a circle, the length of the spring increases due to the increase in centripetal force required to maintain circular motion.
- We have a mass m attached to a spring with a spring constant k. The other end of the spring is held in hand, and the mass is rotated in a horizontal circle.
- The mass experiences a centripetal force that is required to keep it moving in a circular path. This centripetal force is provided by the spring force.
- The centripetal force Fc required to keep the mass moving in a circle of radius r is given by:
Fc=mω2r
where ω is the angular velocity and r is the radius of the circular path.
- The force exerted by the spring when it is stretched by an amount x from its natural length L is given by Hooke's Law:
Fs=kx
- Since the spring provides the centripetal force, we can equate the two forces:
kx=mω2r
- Here, r is the total length of the spring when stretched, which can be expressed as:
r=L+x
- Substitute r into the centripetal force equation:
kx=mω2(L+x)
- Rearranging gives:
kx=mω2L+mω2x
- This can be rearranged to:
kx−mω2x=mω2L
- Factoring out x:
x(k−mω2)=mω2L
- Thus, we can solve for x:
x=mω2Lk−mω2
- The length of the spring when stretched is L+x. As ω increases, mω2 increases, which affects the denominator k−mω2. If mω2 approaches k, x will increase significantly, indicating that the spring stretches more.
- As the mass is whirled in a circle, the length of the spring increases due to the increase in centripetal force required to maintain circular motion.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (VERY SHORT ANSWER QUESTIONS)
7 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (FROM ANGULAR VELOCITY)
4 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
A spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionIf a compressed spring is dissolved in acid, what happens to the elastic potential energy of the spring ?
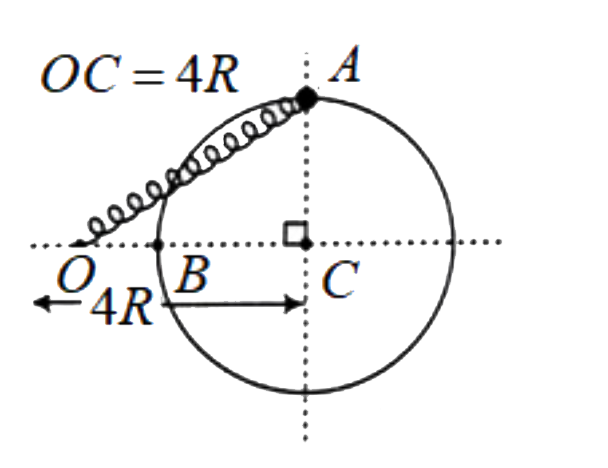
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View SolutionWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

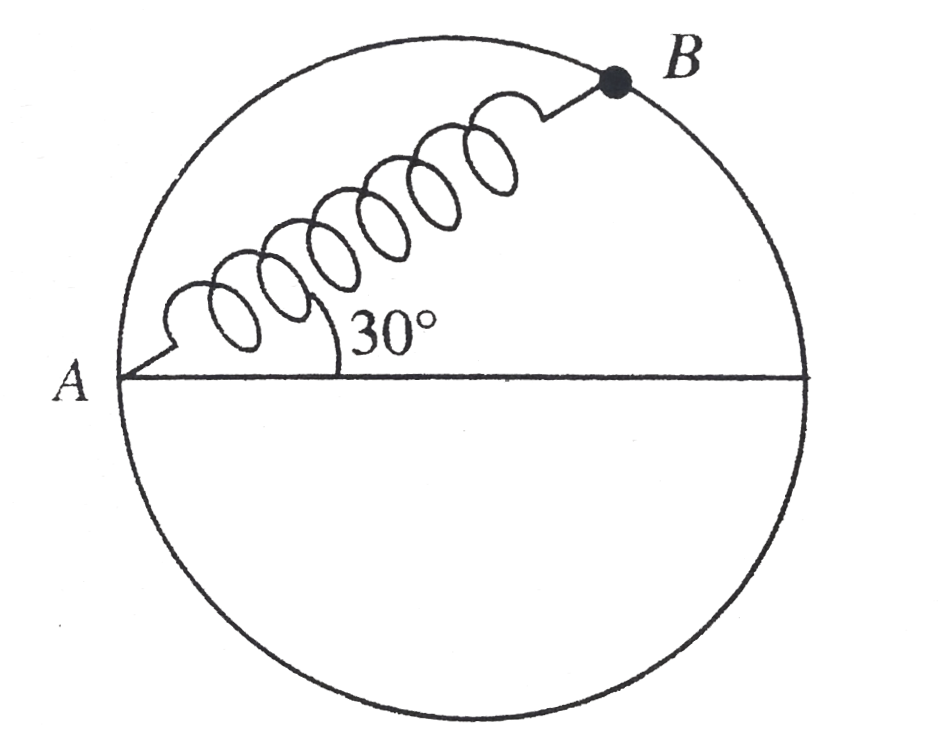
View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
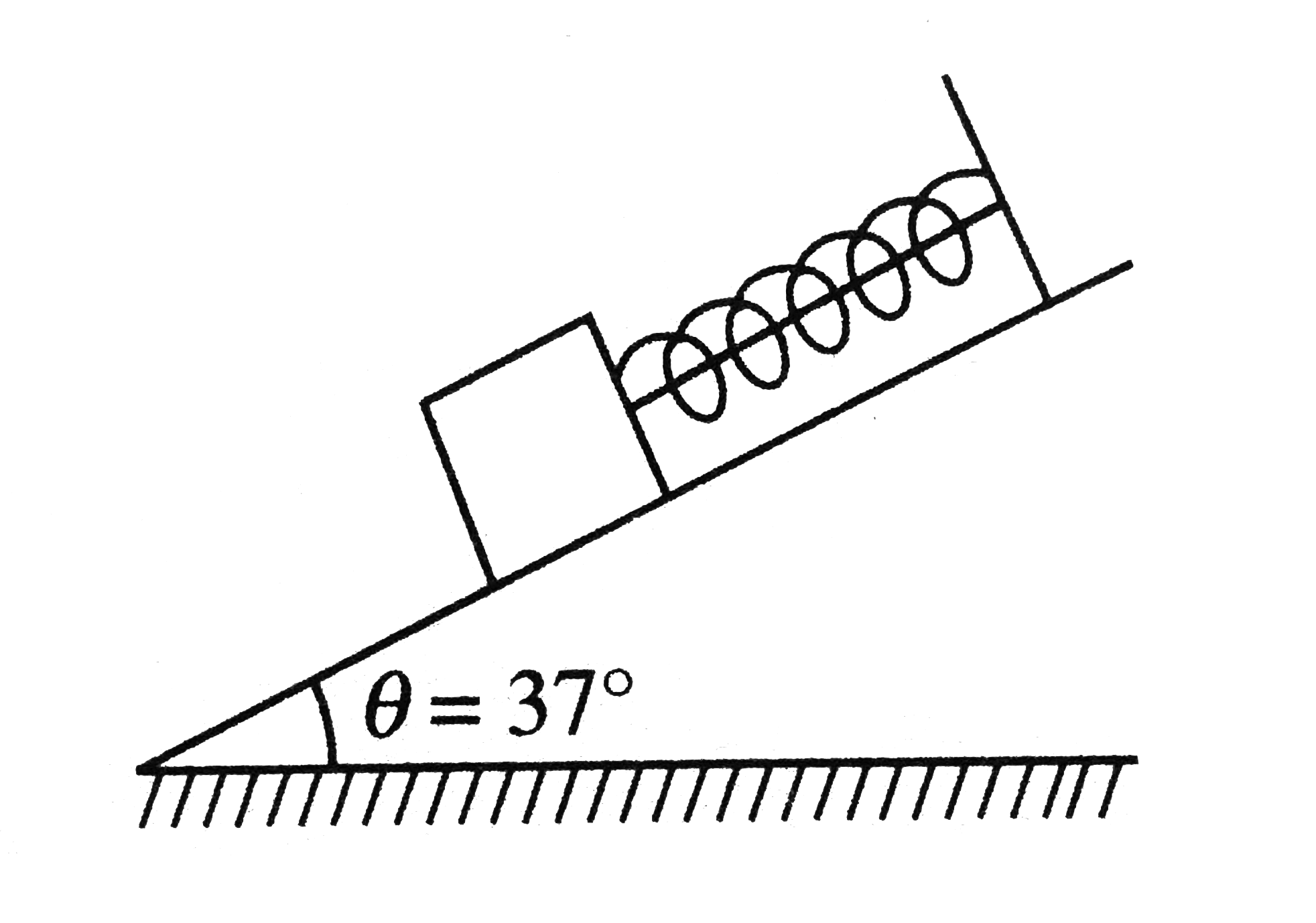
View SolutionA small block of mass m=1kg is attached with one end of the spring of force constant K=110Nm−1. Other end of the spring is fixed to a rough plane having coefficient of friction μ=0.2. The spring is kept in its natural length by an inextensible thread ties between its ends as shown in figure. If the thread is burnt, calculate the elongation of the spring when the block attains static equilibrium position.
View Solution
