At what point does a pilot in an aeroplane appear to be heaviest while performing a loop-the-loop in a vertical plane.
To determine at what point a pilot in an airplane appears to be heaviest while performing a loop-the-loop in a vertical plane, we can analyze the forces acting on the pilot at different points in the loop.
1. Identify the Forces Acting on the Pilot:
- The pilot experiences two main forces:
- The gravitational force (weight), W=mg, acting downward.
- The normal force (N) exerted by the seat, acting upward.
2. Analyze the Situation at Different Points in the Loop:
- The loop-the-loop can be divided into three key points:
- The top of the loop
- The bottom of the loop
- The sides of the loop (left and right)
3. Calculate Forces at the Bottom of the Loop:
- At the bottom of the loop, the forces can be expressed as:
N−mg=mv2R
- Here, N is the normal force, m is the mass of the pilot, g is the acceleration due to gravity, v is the velocity of the airplane, and R is the radius of the loop.
- Rearranging gives:
N=mg+mv2R
- This equation shows that the normal force at the bottom of the loop is the sum of the gravitational force and the centripetal force required to keep the pilot moving in a circular path.
4. Calculate Forces at the Top of the Loop:
- At the top of the loop, the forces can be expressed as:
N+mg=mv2R
- Rearranging gives:
N=mv2R−mg
- Here, the normal force is reduced because both the gravitational force and the centripetal force act in the same direction.
5. Conclusion:
- Comparing the normal forces at the bottom and top of the loop:
- At the bottom: N=mg+mv2R (greater than mg)
- At the top: N=mv2R−mg (can be less than mg)
- Therefore, the pilot feels heaviest at the bottom of the loop because the normal force is maximized there.
Final Answer:
The pilot in an airplane appears to be heaviest at the bottom of the loop while performing a loop-the-loop in a vertical plane.
---
- The pilot experiences two main forces:
- The gravitational force (weight), W=mg, acting downward.
- The normal force (N) exerted by the seat, acting upward.
- The loop-the-loop can be divided into three key points:
- The top of the loop
- The bottom of the loop
- The sides of the loop (left and right)
- At the bottom of the loop, the forces can be expressed as:
N−mg=mv2R
- Here, N is the normal force, m is the mass of the pilot, g is the acceleration due to gravity, v is the velocity of the airplane, and R is the radius of the loop.
- Rearranging gives:
N=mg+mv2R
- This equation shows that the normal force at the bottom of the loop is the sum of the gravitational force and the centripetal force required to keep the pilot moving in a circular path.
- At the top of the loop, the forces can be expressed as:
N+mg=mv2R
- Rearranging gives:
N=mv2R−mg
- Here, the normal force is reduced because both the gravitational force and the centripetal force act in the same direction.
- Comparing the normal forces at the bottom and top of the loop:
- At the bottom: N=mg+mv2R (greater than mg)
- At the top: N=mv2R−mg (can be less than mg)
- Therefore, the pilot feels heaviest at the bottom of the loop because the normal force is maximized there.
The pilot in an airplane appears to be heaviest at the bottom of the loop while performing a loop-the-loop in a vertical plane.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (VERY SHORT ANSWER QUESTIONS)
7 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (FROM ANGULAR VELOCITY)
4 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
A pilot of mass 70 kg in a jet aircraft moves in a vertical circle while executing the loop-the-loop at a constant speed of 200 m/s. If the radius of the circle is 2.5 km what is the force exerted by the seat on the pilot at (a) the top of the loop and (b) the bottom of the loop.
View SolutionA pilot does not fall down when his aeroplane loops the loop. Why ?
View SolutionIf a current of 0.5 apere flows through a metallic wire for 2 hour then how many electrons flow through the wire ?
View SolutionAssertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
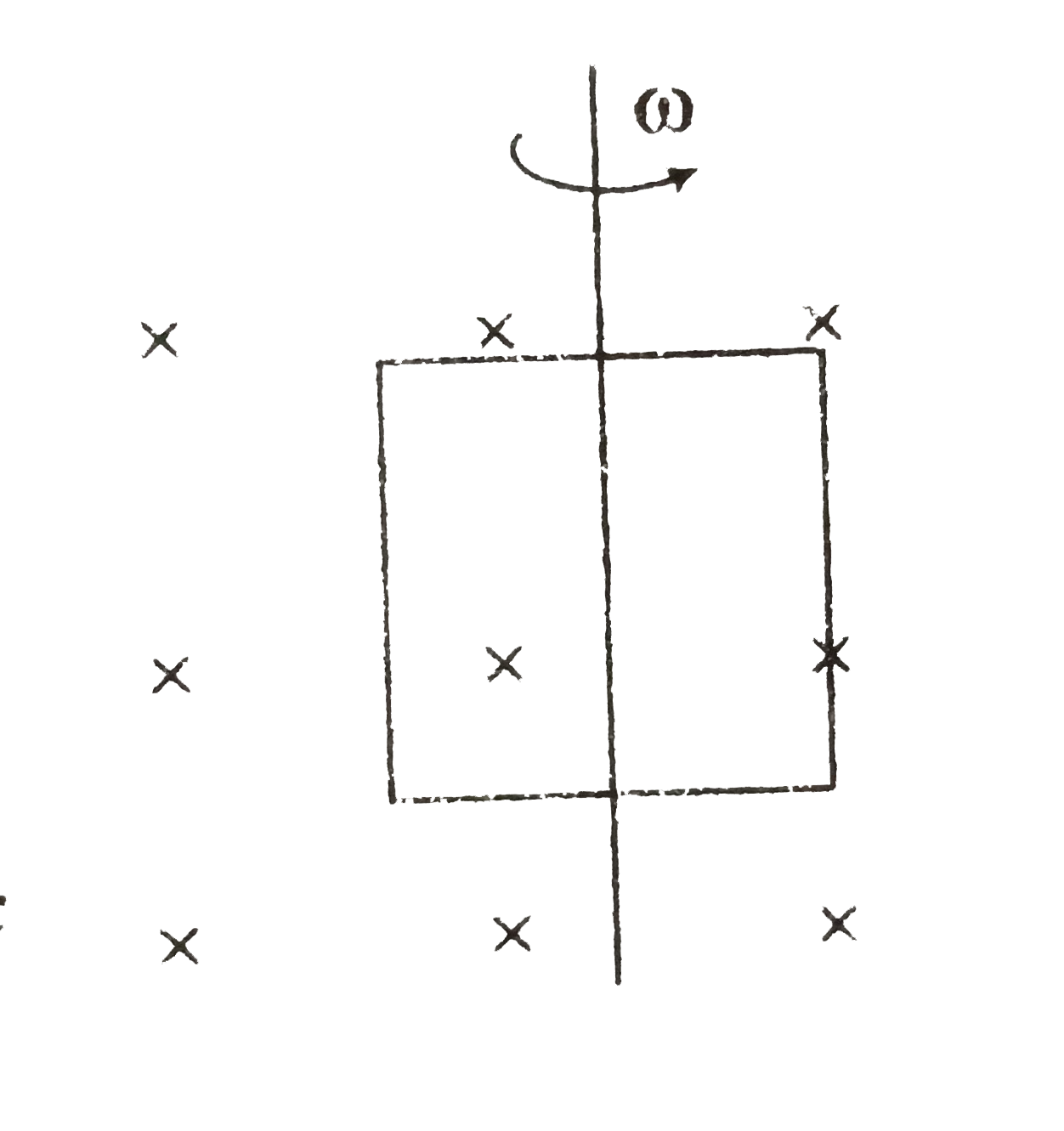
View SolutionIn Fig, find the magnetic field at point P. The loop is lying in x-y plane.

View SolutionA square loop of side l iskept in a uniform magnetic field B such that its plane makes an angle α with →B. The loop carries a current i. The torque experienced by the loop in this position is
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
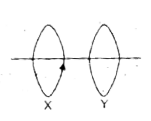
View SolutionThe two loops shown in the figure have their planes parallel to each other . A clockwise current flows in the loop X as viewed from X towards Y. The two coils will repel each other if the current in the loop X is :
View SolutionA circular loop of flexible conducting material is kept in a magnetic field directed perpendicularly into its plane. By holding the loop at diametrically opposite points its is suddenly stretched outwards, then
View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View Solution
