A mass M attached to a spring of spring constant 0.7 N/m oscillates on a smooth horizontal table. When displacement is 0.3 m, velocity is 2 ms−1. And when displacement is 0.4 m, velocity is 0.3 m/s. Calculate the vlaue of M.
To solve the problem, we need to find the mass M attached to a spring with a spring constant k=0.7N/m. We are given two conditions regarding the displacement and velocity of the mass during its oscillation.
1. Identify the Given Values:
- Spring constant, k=0.7N/m
- Condition 1: Displacement x1=0.3m, Velocity v1=2m/s
- Condition 2: Displacement x2=0.4m, Velocity v2=0.3m/s
2. Use the Relationship Between Velocity and Displacement in SHM:
The velocity v of a mass in simple harmonic motion (SHM) is given by:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the displacement.
3. Set Up Equations for Both Conditions:
For the first condition:
2=ω√A2−(0.3)2
Squaring both sides gives:
4=ω2(A2−0.09)(Equation 1)
For the second condition:
0.3=ω√A2−(0.4)2
Squaring both sides gives:
0.09=ω2(A2−0.16)(Equation 2)
4. Rearranging the Equations:
From Equation 1:
ω2A2−0.09ω2=4⇒ω2A2=4+0.09ω2
From Equation 2:
ω2A2−0.16ω2=0.09⇒ω2A2=0.09+0.16ω2
5. Equating the Two Expressions for ω2A2:
Set the two expressions equal to each other:
4+0.09ω2=0.09+0.16ω2
Rearranging gives:
4−0.09=0.16ω2−0.09ω2
3.91=0.07ω2
ω2=3.910.07≈55.8571
6. Relate ω to Mass M:
The angular frequency ω is related to the mass M and the spring constant k by:
ω2=kM
Therefore:
M=kω2=0.755.8571≈0.0125kg
Final Answer:
The mass M is approximately 0.0125kg.
- Spring constant, k=0.7N/m
- Condition 1: Displacement x1=0.3m, Velocity v1=2m/s
- Condition 2: Displacement x2=0.4m, Velocity v2=0.3m/s
The velocity v of a mass in simple harmonic motion (SHM) is given by:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the displacement.
For the first condition:
2=ω√A2−(0.3)2
Squaring both sides gives:
4=ω2(A2−0.09)(Equation 1)
0.3=ω√A2−(0.4)2
Squaring both sides gives:
0.09=ω2(A2−0.16)(Equation 2)
From Equation 1:
ω2A2−0.09ω2=4⇒ω2A2=4+0.09ω2
From Equation 2:
ω2A2−0.16ω2=0.09⇒ω2A2=0.09+0.16ω2
Set the two expressions equal to each other:
4+0.09ω2=0.09+0.16ω2
Rearranging gives:
4−0.09=0.16ω2−0.09ω2
3.91=0.07ω2
ω2=3.910.07≈55.8571
The angular frequency ω is related to the mass M and the spring constant k by:
ω2=kM
Therefore:
M=kω2=0.755.8571≈0.0125kg
The mass M is approximately 0.0125kg.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions)
20 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance
14 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Long Answer Questions)
5 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
A spring of constant k=0.5N/m and an attached mass m oscillates on a smooth horizontal table. When the mass is at position x1=0.1m, its velocity is v1=−1ms−1 , and at x2=0.2m, it has velocity v2=0.5ms−1. Find m and the amplitude A of the motion.
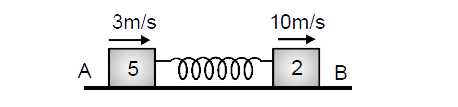
View SolutionTwo blocks A (5kg) and B(2kg) attached to the ends of a spring constant 1120 N/m are placed on a smooth horizontal plane with the spring undeformed. Simultaneously velocities of 3m/s and 10m/s along the line of the spring in the same direction are imparted to A and B then
View Solution
Knowledge Check
A mass m, which is attached to a spring with spring constant k, oscillates on a horizontal table, with amplitude A. At an instant when the spring is streched by √3A/2, a second mass m is dropped vertically onto the original mass and immediately sticks to it. what is the amplitude of the resulting motion-
A√32AB√78AC√1316AD√23AA 0.20kg object mass attached to a spring whose spring constant is 500N/m executes simple harmonic motion. If its maximum speed is 5.0m/s, the amplitude of its oscillation is
A0.0020mB0.10mC0.20mD25ma block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2J
Two blocks A(5kg) and B(2kg) attached to the ends of a spring constant 1120N/m are placed on a smooth horizontal plane with the spring undeformed. Simultaneously velocities of 3m/s and 10m/s along the line of the spring in the same direction are imparted to A and B then

View SolutionTwo blocks A (5kg) and B (2kg) attached to the ends of a spring constant 1120 N/m are placed on a smooth horizontal plane with the spring unreformed. Simulataneously velocities of 3 m/s and 10 m/s along the line of the spring in the same direction are imparted to A and B then

View SolutionA 1.2kg mass is oscillating without friction on a spring whose spring constant is 3400N/m. When the mass's displacement is 7.2cm. What is its acceleration?
View SolutionTwo blocks A(5kg) and B(5kg) attached to the ends of a spring constant 1000N/m are placed on a smooth horizontal plane with the spring undeformed . Simultaneously velocities of 10m/s and 4m/s along the line of the spring in the same direction are imparted toA and B then
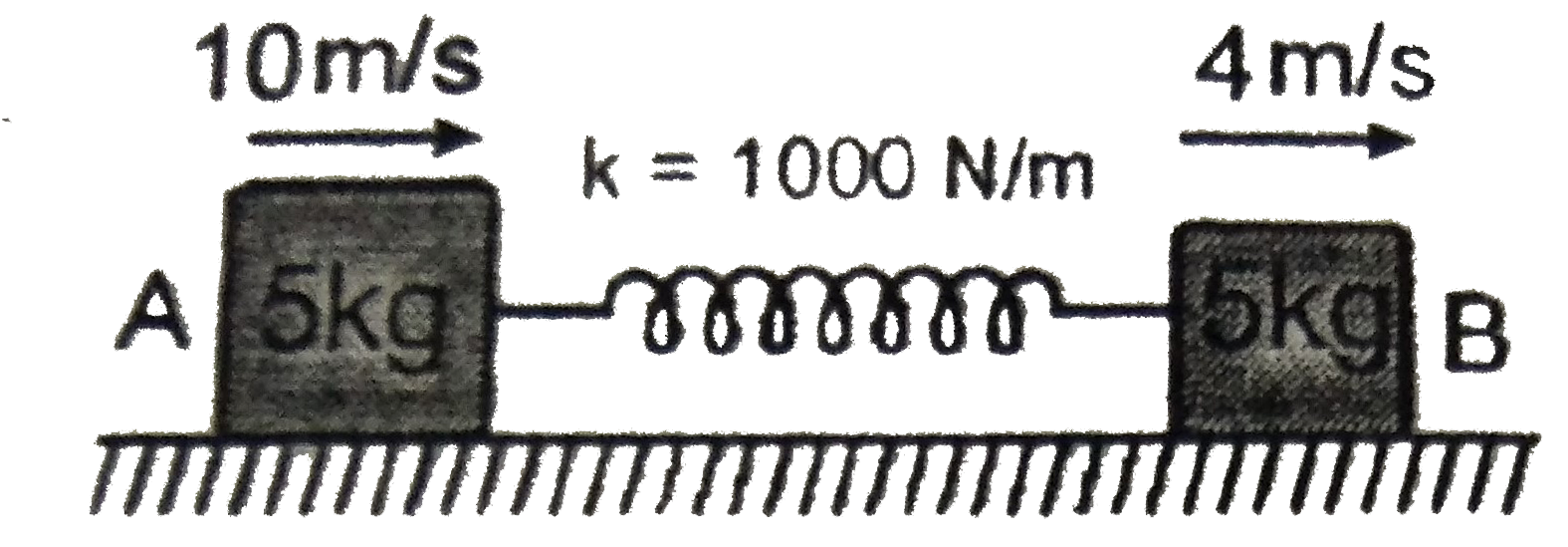
View SolutionA particle of mass 0.25 kg vibrates with a period of 2 s. It its greatest displacement is 0.4 m, its maximum velocity in m/s will be
View Solution
