A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is

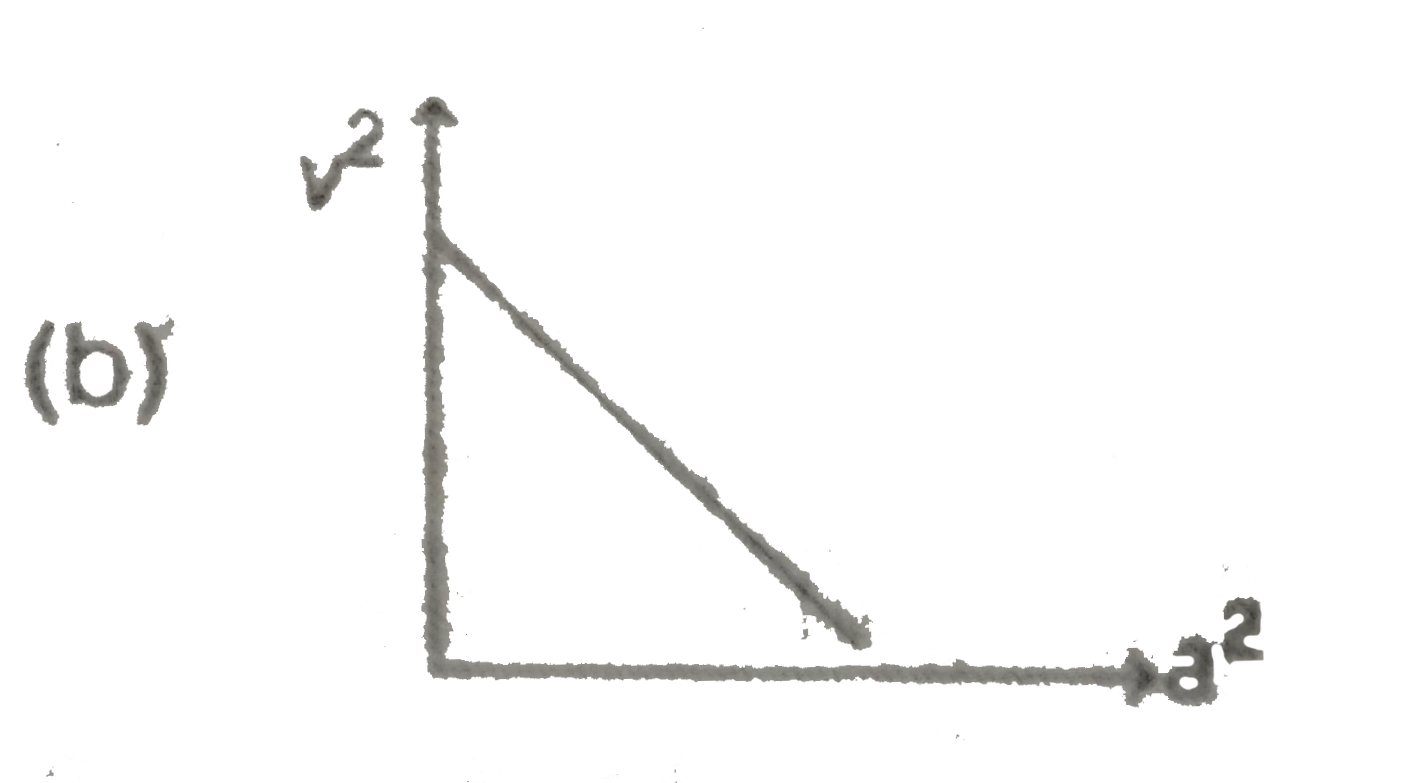


The correct Answer is:B
To solve the problem of identifying the correct graph for acceleration a and corresponding linear velocity v of a mass performing linear simple harmonic motion (SHM), we can follow these steps:
Step 1: Understand the equations of SHM
The displacement x of a mass in SHM can be expressed as:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
Step 2: Derive the velocity equation
To find the velocity v, we differentiate the displacement with respect to time:
v(t)=dxdt=Aωcos(ωt)
Step 3: Derive the acceleration equation
Next, we differentiate the velocity to find the acceleration a:
a(t)=dvdt=−Aω2sin(ωt)
This can also be expressed in terms of displacement:
a=−ω2x
Step 4: Relate acceleration and velocity
From the equations derived, we have:
- v=Aωcos(ωt)
- a=−ω2Asin(ωt)
Step 5: Express v2 and a2
From the equations, we can express v2 and a2:
v2=(Aωcos(ωt))2=A2ω2cos2(ωt)
a2=(−ω2Asin(ωt))2=ω4A2sin2(ωt)
Step 6: Use the identity sin2+cos2=1
Using the identity sin2(θ)+cos2(θ)=1, we can relate v2 and a2:
v2A2ω2+a2ω4A2=1
Rearranging gives:
v2=A2ω2−a2ω4A2ω2
This shows that v2 is a linear function of a2 with a negative slope.
Step 7: Identify the graph
The relationship derived indicates that as a2 increases, v2 decreases, which corresponds to a straight line with a negative slope. Therefore, the correct graph will show v2 on the y-axis and a2 on the x-axis, with a negative slope.
Conclusion
Based on the analysis, the correct option for the graph of acceleration a and corresponding linear velocity v is the one that shows a linear relationship with a negative slope.
---
The displacement x of a mass in SHM can be expressed as:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
To find the velocity v, we differentiate the displacement with respect to time:
v(t)=dxdt=Aωcos(ωt)
Next, we differentiate the velocity to find the acceleration a:
a(t)=dvdt=−Aω2sin(ωt)
This can also be expressed in terms of displacement:
a=−ω2x
From the equations derived, we have:
- v=Aωcos(ωt)
- a=−ω2Asin(ωt)
From the equations, we can express v2 and a2:
v2=(Aωcos(ωt))2=A2ω2cos2(ωt)
a2=(−ω2Asin(ωt))2=ω4A2sin2(ωt)
Using the identity sin2(θ)+cos2(θ)=1, we can relate v2 and a2:
v2A2ω2+a2ω4A2=1
Rearranging gives:
v2=A2ω2−a2ω4A2ω2
This shows that v2 is a linear function of a2 with a negative slope.
The relationship derived indicates that as a2 increases, v2 decreases, which corresponds to a straight line with a negative slope. Therefore, the correct graph will show v2 on the y-axis and a2 on the x-axis, with a negative slope.
Based on the analysis, the correct option for the graph of acceleration a and corresponding linear velocity v is the one that shows a linear relationship with a negative slope.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Only one question is correct
48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
View SolutionWhile a particle executes linear simple harmonic motion
View SolutionFor a particle executing simple harmonic motion, the acceleration is -
View SolutionFor a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionAssertion: In simple harmonic motion the velocity is maximum when the acceleration is minimum
Reason : Displacement and velocity of SHMdiffer in phase by π2
View Solution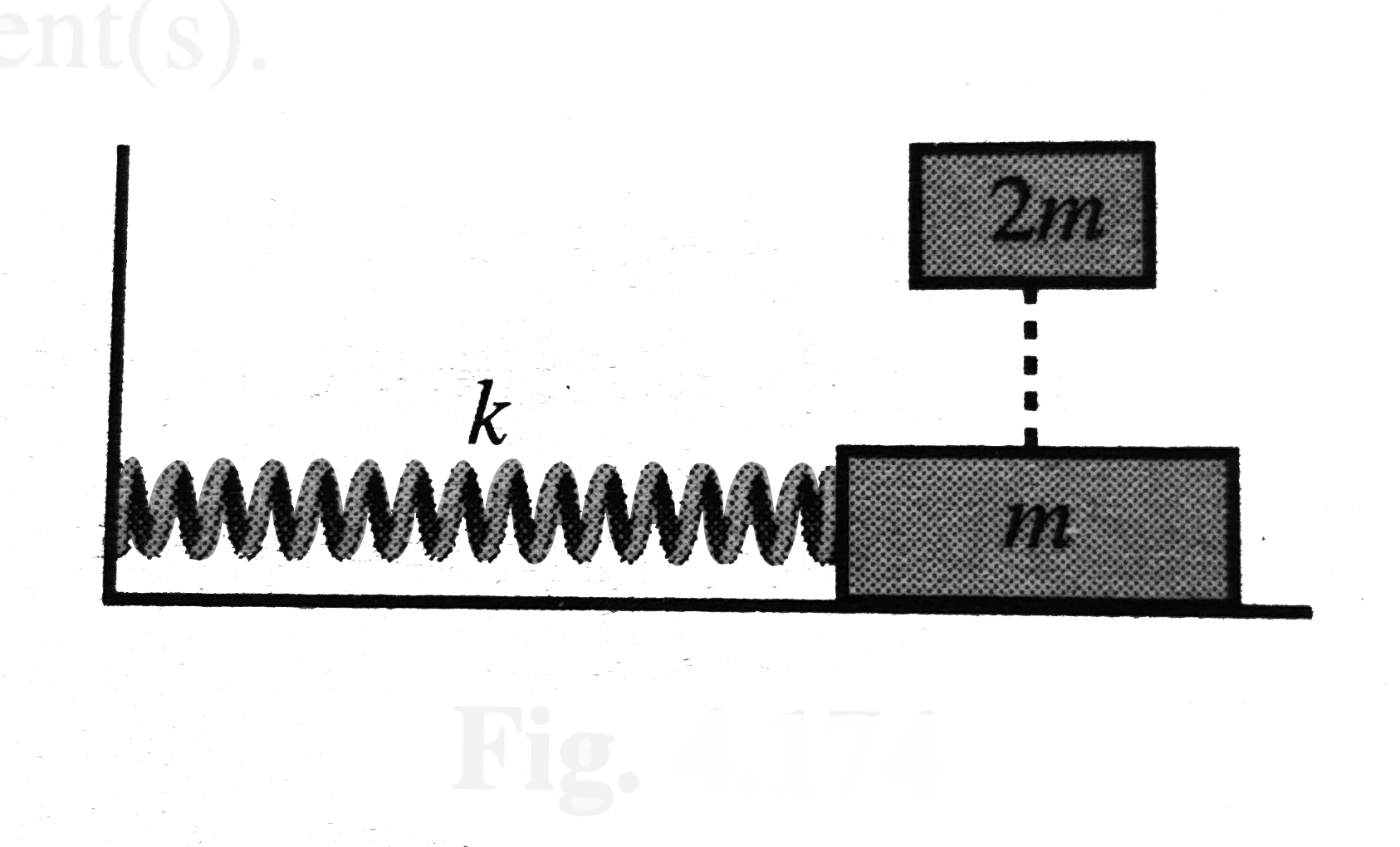
An object of mass m is performing simple harmonic motion on a smooth horizontal surface as shown in Fig. just as the oscillating object reaches its extreme position, another object of mass 2 m is dropped on to oscillating object, which sticks to it. For this situation mark out the correct statement (s).
View SolutionA particle is executing a simple harmonic motion. Its maximum acceleration is α and maximum velocity is β. Then, its time period of vibration will be
View SolutionA body is performing simple harmonic motion with amplitude a and time period T variation of its acceleration (f) with time(t) is shown in figure If at time t velocity of the body is v which of the following graph is correct?

View SolutionA body is performing simple harmonic motion with amplitude a and time period T variation of its acceleration (f) with time(t) is shown in figure If at time t velocity of the body is v which of the following graph is correct?

View SolutionA block performs simple harmonic motion with equilibrium point x = 0 . Graph of acceleration of the block as a function of time is shown. Which of the following statement is correct about the block ?

View Solution
