A particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x2=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/s2)
2 rad/s
4 rad/s
6 rad/s
8 rad/s
The correct Answer is:A
To solve the problem of finding the angular frequency of oscillation of a particle placed at the lowest point of a smooth wire frame in the shape of a parabola, we can follow these steps:
Step 1: Understand the Parabola Equation
The equation of the parabola given is x2=5y. This represents a parabola that opens upwards with its vertex at the origin (0,0).
Step 2: Identify the Lowest Point
The lowest point of the parabola is at the origin (0,0). When the particle is at this point and is slightly displaced, it can oscillate about this point.
Step 3: Determine the Slope of the Parabola
To find the slope of the parabola at any point, we differentiate the equation y=x25:
dydx=2x5
At the lowest point (x = 0), the slope is dydx=0.
Step 4: Analyze Forces Acting on the Particle
When the particle is displaced by a small angle θ, the gravitational force mg acts downwards. The component of this force acting along the slope of the parabola can be expressed as:
F=−mgsin(θ)
For small angles, we can approximate sin(θ)≈θ.
Step 5: Relate the Angle to Displacement
From the slope of the parabola, we have:
tan(θ)=dydx=2x5
For small angles, tan(θ)≈θ, thus:
θ≈2x5
Step 6: Set Up the Equation of Motion
The force acting on the particle can be written as:
F=−mgθ
Substituting θ from the previous step:
F=−mg(2x5)
Using Newton's second law F=ma, where a=d2xdt2:
md2xdt2=−mg(2x5)
Dividing through by m:
d2xdt2=−g(2x5)
Step 7: Substitute the Value of g
Given g=10m/s2:
d2xdt2=−10(2x5)=−4x
Step 8: Identify the Angular Frequency
This equation can be compared to the standard form of simple harmonic motion:
d2xdt2=−ω2x
From our equation, we have:
ω2=4
Thus, the angular frequency ω is:
ω=√4=2rad/s
Final Answer
The angular frequency of oscillation is ω=2rad/s.
---
The equation of the parabola given is x2=5y. This represents a parabola that opens upwards with its vertex at the origin (0,0).
The lowest point of the parabola is at the origin (0,0). When the particle is at this point and is slightly displaced, it can oscillate about this point.
To find the slope of the parabola at any point, we differentiate the equation y=x25:
dydx=2x5
At the lowest point (x = 0), the slope is dydx=0.
When the particle is displaced by a small angle θ, the gravitational force mg acts downwards. The component of this force acting along the slope of the parabola can be expressed as:
F=−mgsin(θ)
For small angles, we can approximate sin(θ)≈θ.
From the slope of the parabola, we have:
tan(θ)=dydx=2x5
For small angles, tan(θ)≈θ, thus:
θ≈2x5
The force acting on the particle can be written as:
F=−mgθ
Substituting θ from the previous step:
F=−mg(2x5)
Using Newton's second law F=ma, where a=d2xdt2:
md2xdt2=−mg(2x5)
Dividing through by m:
d2xdt2=−g(2x5)
Given g=10m/s2:
d2xdt2=−10(2x5)=−4x
This equation can be compared to the standard form of simple harmonic motion:
d2xdt2=−ω2x
From our equation, we have:
ω2=4
Thus, the angular frequency ω is:
ω=√4=2rad/s
The angular frequency of oscillation is ω=2rad/s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Only one question is correct
48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
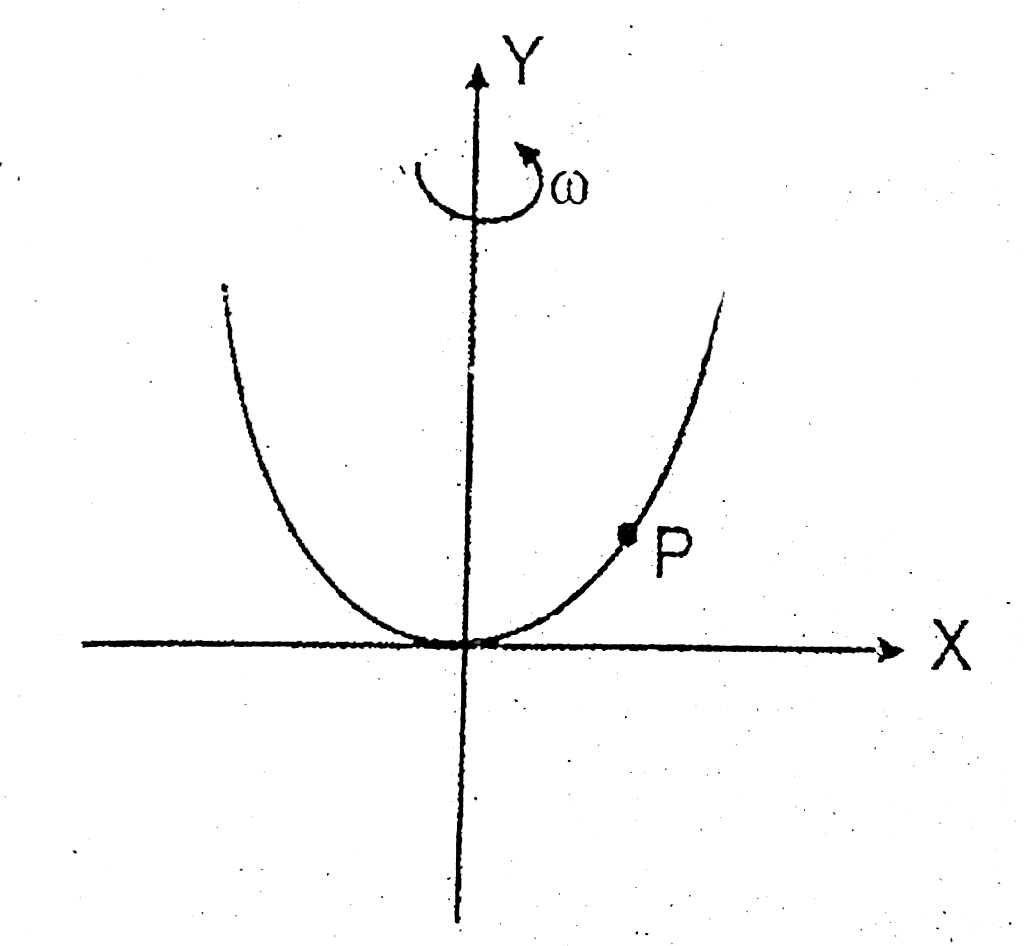
A smooth wire frasme is in the shape of a parabola y=5x2 . It is being rotated about y-axis with an angular velocity ω. A small bead of mass (m=1kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity ω is (g=10m/s2)
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
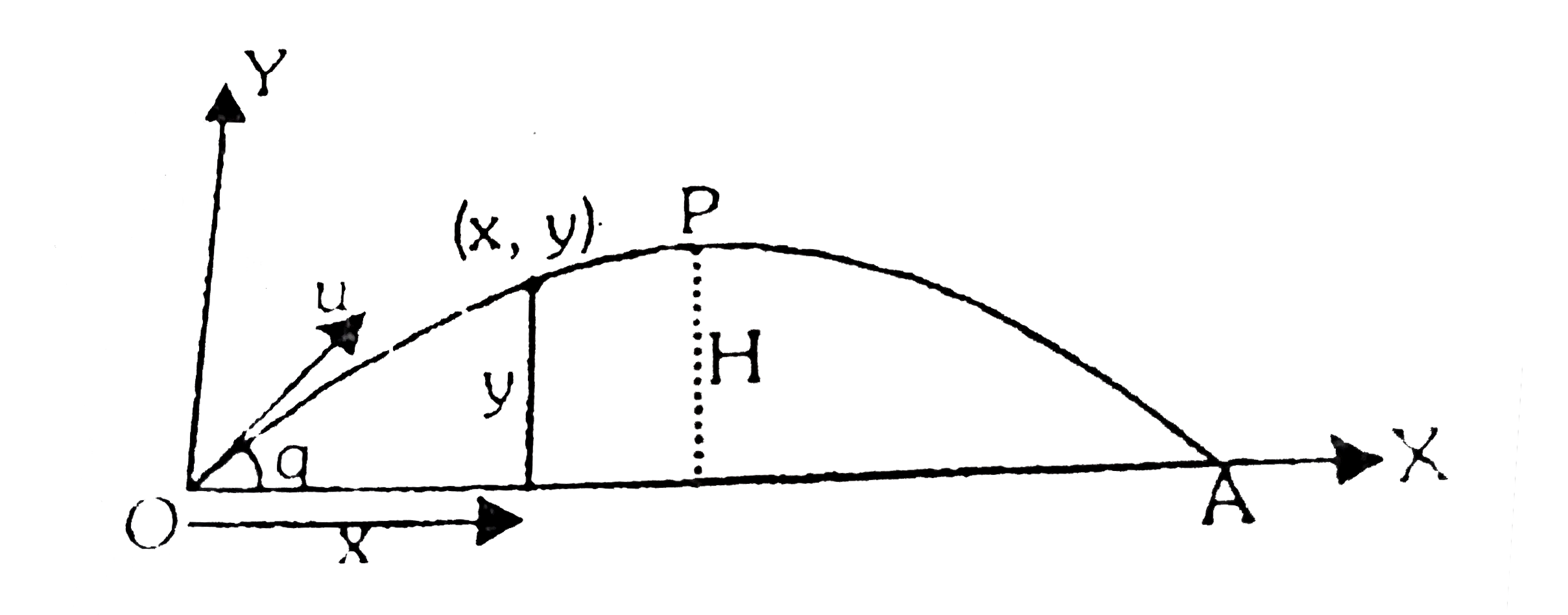
Range OA is :-
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
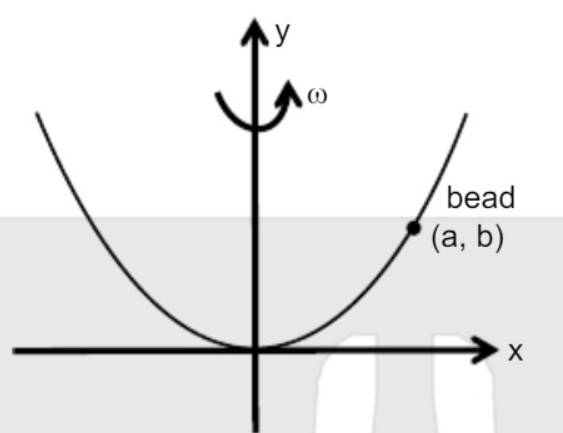
View SolutionAngular velocity of smooth parabolic wire y = 4c(x)^(2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Maximum height H is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-
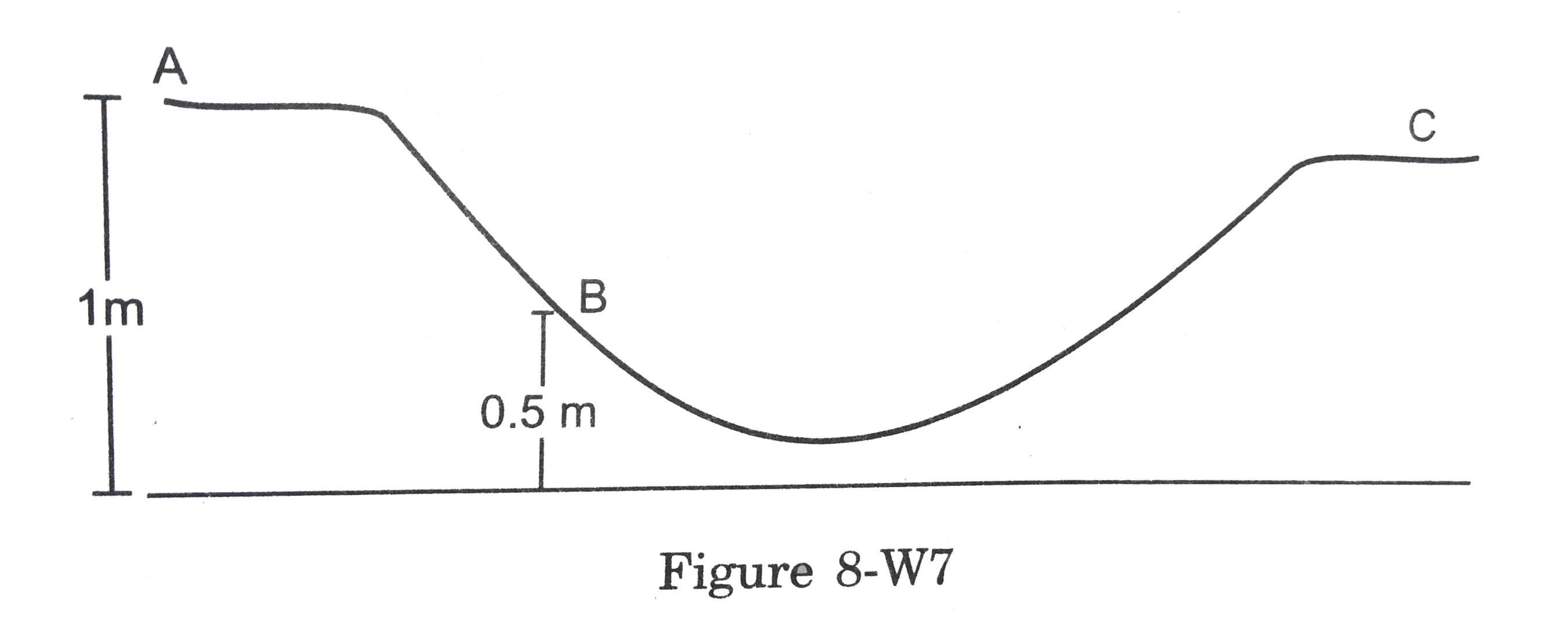
View SolutionA particle is placed at the point A of a frictionless track ABC as shown in figure. It is pushed slightly towards right. Find its speed when it reches the point B. Take g=10ms2.
View SolutionThe x and y coordinates if the particle at any time are x=5t−2t2 and t = 10t respectively, where x and y are in meters and t in second.The acceleation of the aprticle at t = 2 s is
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View SolutionA bead of mass m slides down a frictionless thin fixed wire held on the vertical plane and then performs small oscillations at the lowest point O of the wire. The wire takes the shape of a parabola near O and potential energy is given by U (x)=cx2, where c is a constant. The period of the small oscillations will be :

View Solution
