A mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constant are k 1 and k 2 respectively. When set into vertical vibrations, the period will be 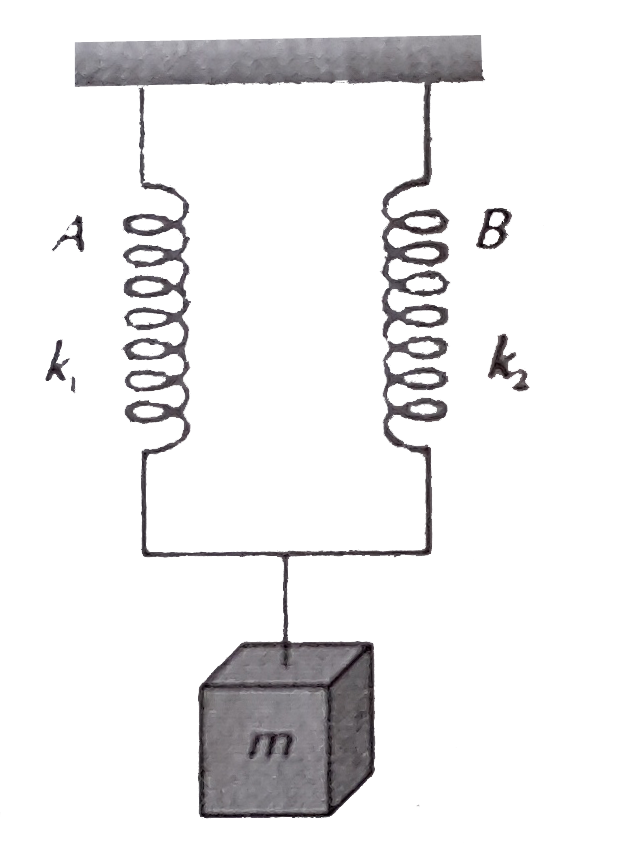
2π√(mk1k2)
2π√m(k1k2)
2π√mk1−k2
2π√mk1+k2
The correct Answer is:D
Step by step video, text & image solution for A mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constant are k 1 and k 2 respectively. When set into vertical vibrations, the period will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Superposition of S.H. M and Resonance
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Graphical Questions
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple pendulum
61 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- SURFACE TENSIONBOOK - ERRORLESS CHAPTER - SURFACE TENSIONEXERCISE - Exercise
214 Videos
Similar Questions
Knowledge Check
A mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are k1andk2 respectively. When set into vertical vibrations, the period will be
 A2π√(mk1k2)B2π√m(k1k2)C2π√(mk1−k2)D2π√(mk1+k2)
A2π√(mk1k2)B2π√m(k1k2)C2π√(mk1−k2)D2π√(mk1+k2)A mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
AT=2π√mk1−k2BT=2π√mk1k2k1+k2CT=2π√mk1+k2DT=2π√m(k1+k2)k1k2Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be
A8π√k1+k2k1k2Bπ2√k1k2C√k1+k28πDπ√k1−k22
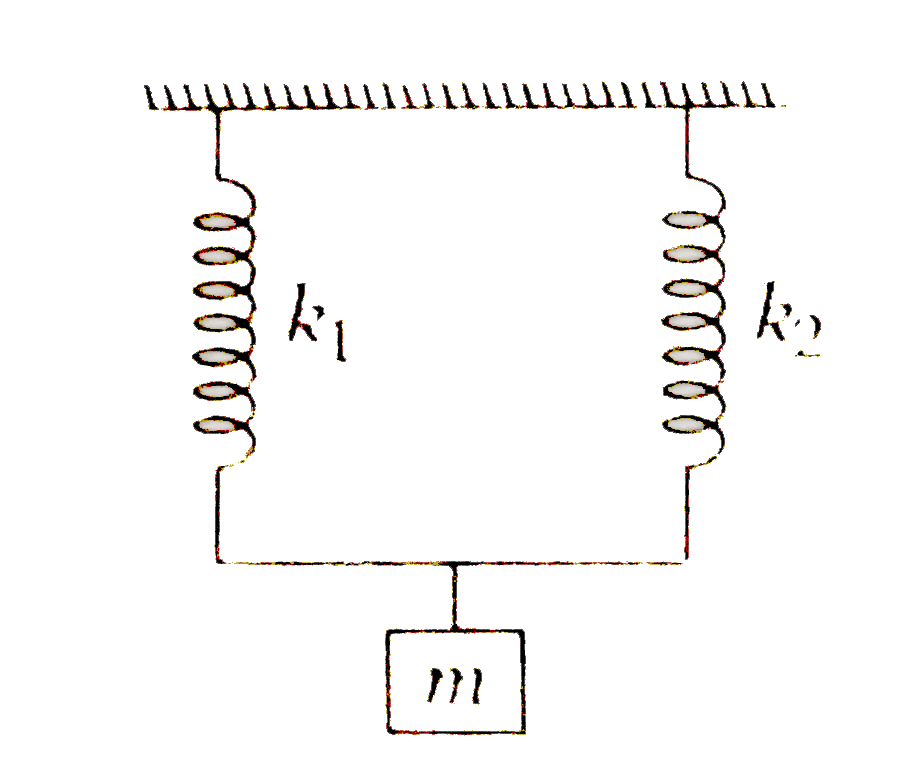
The spring constants of two springs of same length are k1 and k2 as shown in figure. If an object of mass m is suspended and set in vibration , the period will be
View SolutionTwo springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two springs are K1 and K2 respectively. The period of vertical oscillations of the system will be:
View SolutionThe mass in the figure can slide on a frictionless surface. When the mass is pulled out, spring 1 is stretched a distance x1and spring 2 is stretched a distance x2. The spring constants are k1andk2 respectively. Magnitude of spring force pulling back on the mass is

View SolutionTwo springs have their force constant as k1 and k2(k1>k2). When they are streched by the same force.
View SolutionA mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is

View Solution

