A mass m = 100 gm is attached at the end of a light spring which oscillates on a frictionless horizontal table with an amplitude equal to 0.16 metre and time period equal to 2 sec. Initially the mass is released from rest at t = 0 and displacement x = –0.16 metre. The expression for the displacement of mass at any time t is
x=0.16cos(πt)
x=−0.16cos(πt)
x=0.16cos(πt+π)
x=−0.16cos(πt+π)
The correct Answer is:B
Step by step video, text & image solution for A mass m = 100 gm is attached at the end of a light spring which oscillates on a frictionless horizontal table with an amplitude equal to 0.16 metre and time period equal to 2 sec. Initially the mass is released from rest at t = 0 and displacement x = –0.16 metre. The expression for the displacement of mass at any time t is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Superposition of S.H. M and Resonance
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Graphical Questions
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple pendulum
61 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- SURFACE TENSIONBOOK - ERRORLESS CHAPTER - SURFACE TENSIONEXERCISE - Exercise
214 Videos
Similar Questions
A mass of 2 kg is attached to the spring constant 50Nm−1. The block is pulled to a distance of 5cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA body of mass m attached to a spring which is oscillating with time period 4 seconds. If the mass of the body is increased by 4kg, Its timer period increases by 2sec. Determine value of initial mass m.
View Solution
Knowledge Check
A mass m=100 gram is attached at the end of a light spring which oscillates on a frictionless horizontal table with an amplitude equalt to 0.16m and time period equal to 2 second. Initially the mass is released from rest at t=0 and displacement x=−0.16 metre. The expression for the displacement of mass at any time (t) is
Ax−0.16cos(πt)Bx=−0.16cos(πt)Cx=0.16cos(πt+π)Dx=−0.16cos(πt+π)A particle of 0.8 kg is executing S.H.M., Its amplitude is 1.0 metre and time period is 117 seconds. The velocity of the particle at the instant when its displacement is 0.6 metre will be :
A32 m/sB3.2 m/sC0.32 m/sDzeroA bead of mass m is attached to the mid-point of a taut, weightless string of length l and placed on a frictionless horizontal table.
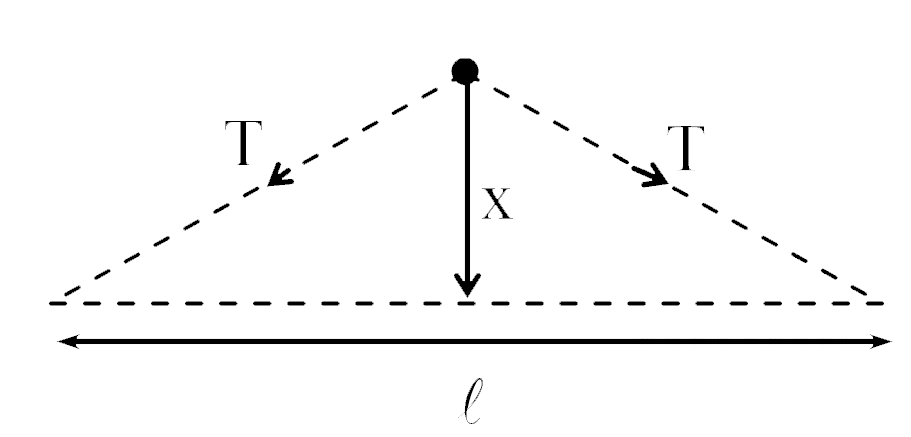
Under a small transverse displacement x, as shown, if the tension in the string is T, then the frequency of oscillation is-A12π√2TmlB12π√4TmlC12π√4TmD12π√2Tm
A mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
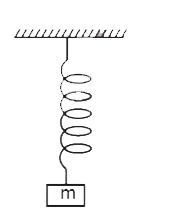
View SolutionTwo masses m1andm2 re connected by a spring of spring constnt k and are placed on as frictionless horizontal surface. Initially the spring is tretched through a distance x0 when the system is released from rest. Find the distance moved by the tow masses before they again come to rest.
View SolutionA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionTwo masses m1 and m2 connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
View SolutionA body of mass 36 g moves with S.H.M. of amplitude A = 13 cm and time period T = 12 s. At time t = 0, the displacement x is + 13 cm. The shortest time of passage from x = + 6.5 cm to x = - 6.5 cm is
View Solution
