A mass on the end of a spring undergoes simple harmonic motion with a frequency of 0.5 Hz. If the attached mass is reduced to one quarter of its value, then the new frequency in Hz is
0.25
The correct Answer is:B
Step by step video, text & image solution for A mass on the end of a spring undergoes simple harmonic motion with a frequency of 0.5 Hz. If the attached mass is reduced to one quarter of its value, then the new frequency in Hz is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
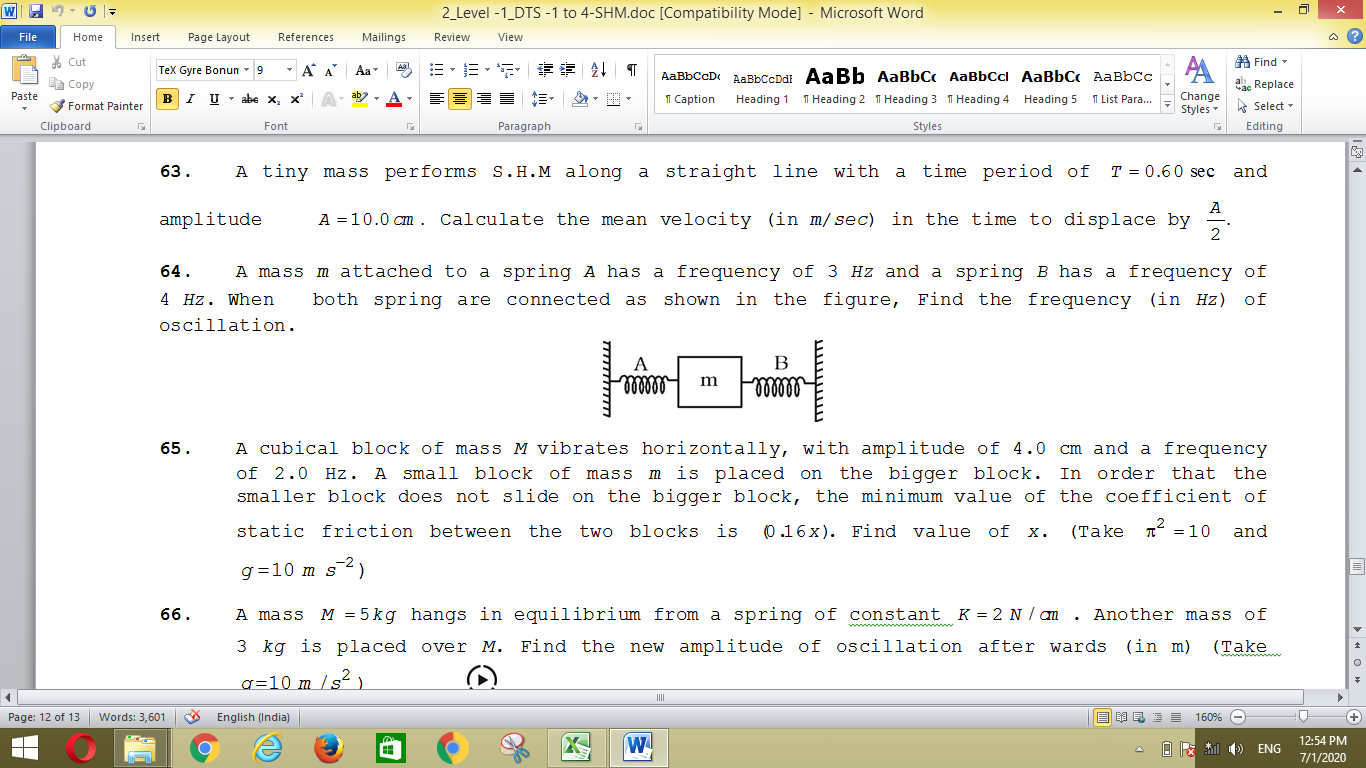
A mass m attached to a spring A has a frequency of 3 Hz and a spring B has a frequency of 4 Hz.When both spring are connected as shown in the figure, Find the frequency (in Hz)of oscillation.
View SolutionA body is executing simple harmonic motion with frequency 'n' the frequency of its potential energy is
View Solution
Knowledge Check
A particle executes simple harmonic motion with a frequency f. The frequency with which its kinetic energy oscillates is
Af// 2BfC2 fD4 fA particle executes simple harmonic motion with a frequency f. The frequency with which its kinetic energy oscillates is
Af2BfC2 fD4 fA body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1
A particle is executing simple harmonic motion with frequency f . The frequency at which its kinetic energy changes into potential energy is
View SolutionIf the period of a simple pendulum is 2s, then its frequency is 0.5Hz
View SolutionIn an open organ pipe the fundamental frequency is 30 Hz.
If the organ pipe is closed at one end, then the fundamental frequency will be
View SolutionAn organ pipe closed at one end has a harmonic with a frequency of 500 Hz. The next higher harmonic in an organ pipe closed at one end but of double length has frequency 350 Hz. Which of the following option is correct? (speed of sound in air is 340m/s)
View SolutionA 1 cm long string vibrates with fundamental frequency of 256 Hz . If the length is reduced to 14 cm keeping the tension unaltered, the new fundamental frequency will be
View Solution
