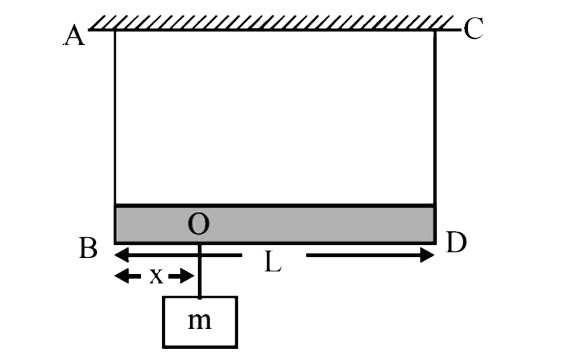
A massless rod of length is suspended by two identical string and of equal length. A block of mass is suspended from point such that is equal to 'x'. Further it is observed that the frequency of harmonic in is equal to harmonic frequency in . 'x' is
The correct Answer is:A
Frequency of the first harmonic of
, When is the length of the two strings.
Frequency of the 2nd harmonic of CD
Given that the two frequencies are equal.
...(ii)
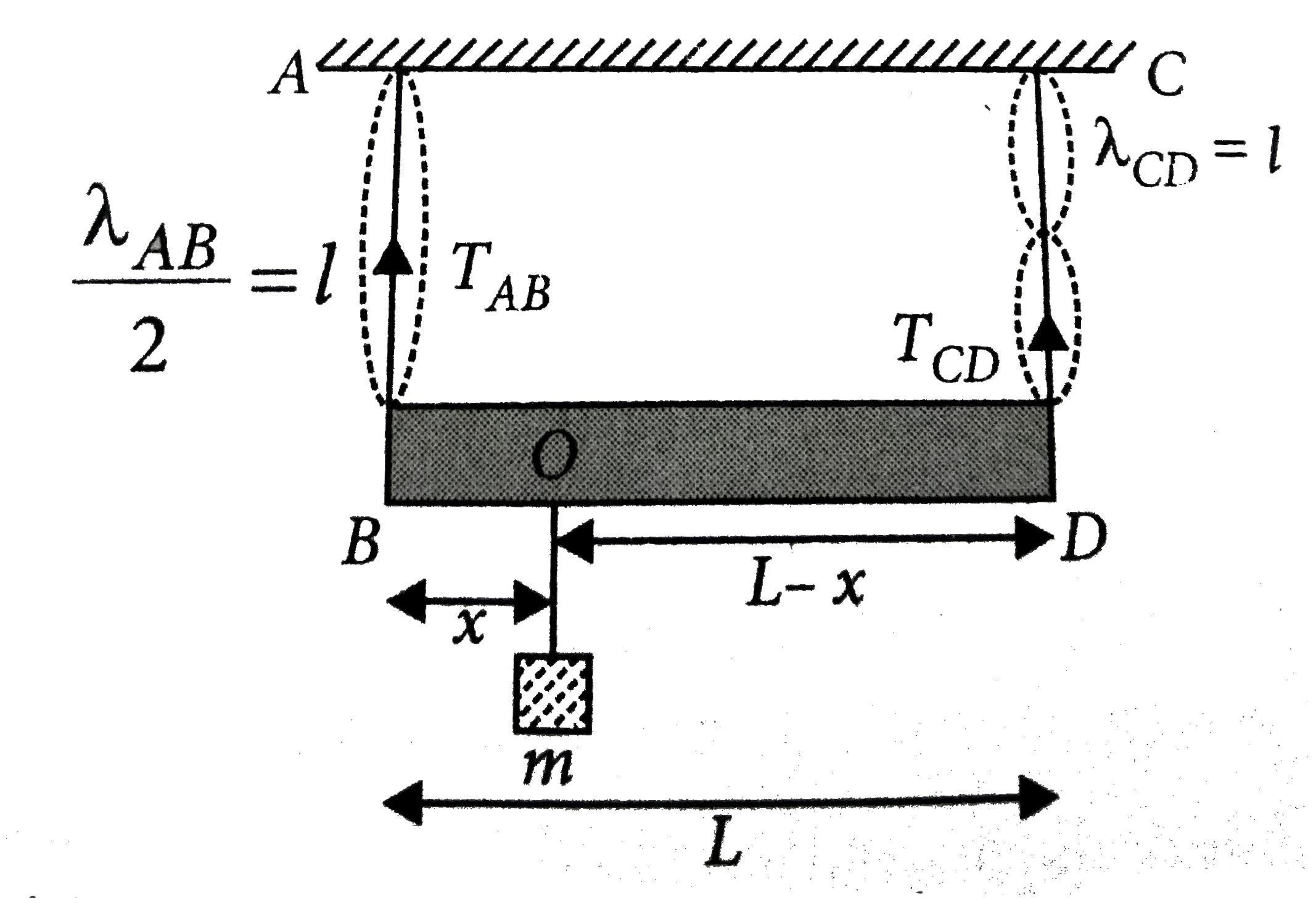
For rotation equilibrium of masscles rod taking torque about point O.
...(iii)
Solve to get,
Topper's Solved these Questions
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - NCERT Exemplar
10 Videos
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - Doppler Effect
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTIPSCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason
15 Videos
Similar Questions
A massless rod is suspended by two identical strings AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to ‘x’. Further, it is observed that the frequency of 1st harmonic (fundamental frequency) in AB is equal to 2nd harmonic frequency in CD. Then, length of BO is

View SolutionA uniform rod of mass m and length L is suspended through two vertical strings of equal lengths fixed at ends. A small object of mass 2m is placed at distance L/4 from the left end. Find the tensions in the two strings.
View Solution
Knowledge Check
A massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal ti 'x'. Further it is obsreved that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD. 'x' is
 A(a) L5B(b) 4L5C( c ) 3L4D(d) L4
A(a) L5B(b) 4L5C( c ) 3L4D(d) L4A massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png) Al5Bl4C4l5D3l4
Al5Bl4C4l5D3l4A light rod of length L is suspended from a support horizonatlly by means of two vertical wires A and B of equal lengths as show in the figure . Cross-section area of A is half that of B and Young's modulus of A is double than that
A20m/sB25m/sC22m/sD18m/s
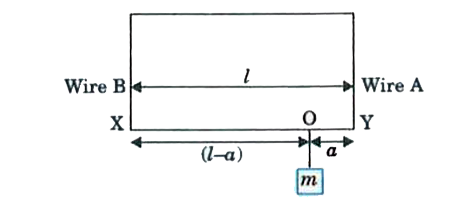
From two identical wires, a rod XY of length l is hung. A wooden block of mass m is hung at point O of the rod at a distance a from wire A. Find the value of a in the case when a tuning fork excites the fundamental note in wire A and third harmonic in wire B.
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png)
View SolutionA spring has a force constant k and a mass m is suspended from it the spring is cut in two equal halves and the same mass is suspended from one of the halves. If the frequency of oscillation in the first case is n, then the frequency in the second case will be
View SolutionA uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :

View SolutionA uniform rod of length 15 cm is suspended from a fixed point by two strings of length 9 cm and 12 cm attached at its ends. If the inclination of the rod to the vertical is θ then sinθ is equal to
View Solution
