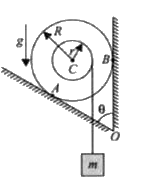
A massless spool of inner radius r outer radius R is placed against a vertical wall and a titled split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass m is hainging. There exists no friction at point A, while the coefficient of friction between the spool and point B is μ. The angle between the two surface is ρ

The magnitude of the force on the spool at B in order to maintain equilibrium is mg√(rR)2+(1−rR)21tan2θ
The magnitude of the force on the spool at B in order to maintain equilibrum is mg(1−rR)1tanθ
The minimum value of μ for the system to remain in equilibrium is cotθ(R/r)−1
The minimum values of μ for the system to remain in equilibrium is tanθ(R/r)−1
The correct Answer is:A, D
mgr=fR………..i
N1sinθ+f=mg ………………ii
N1cosθ=N2……………..iii
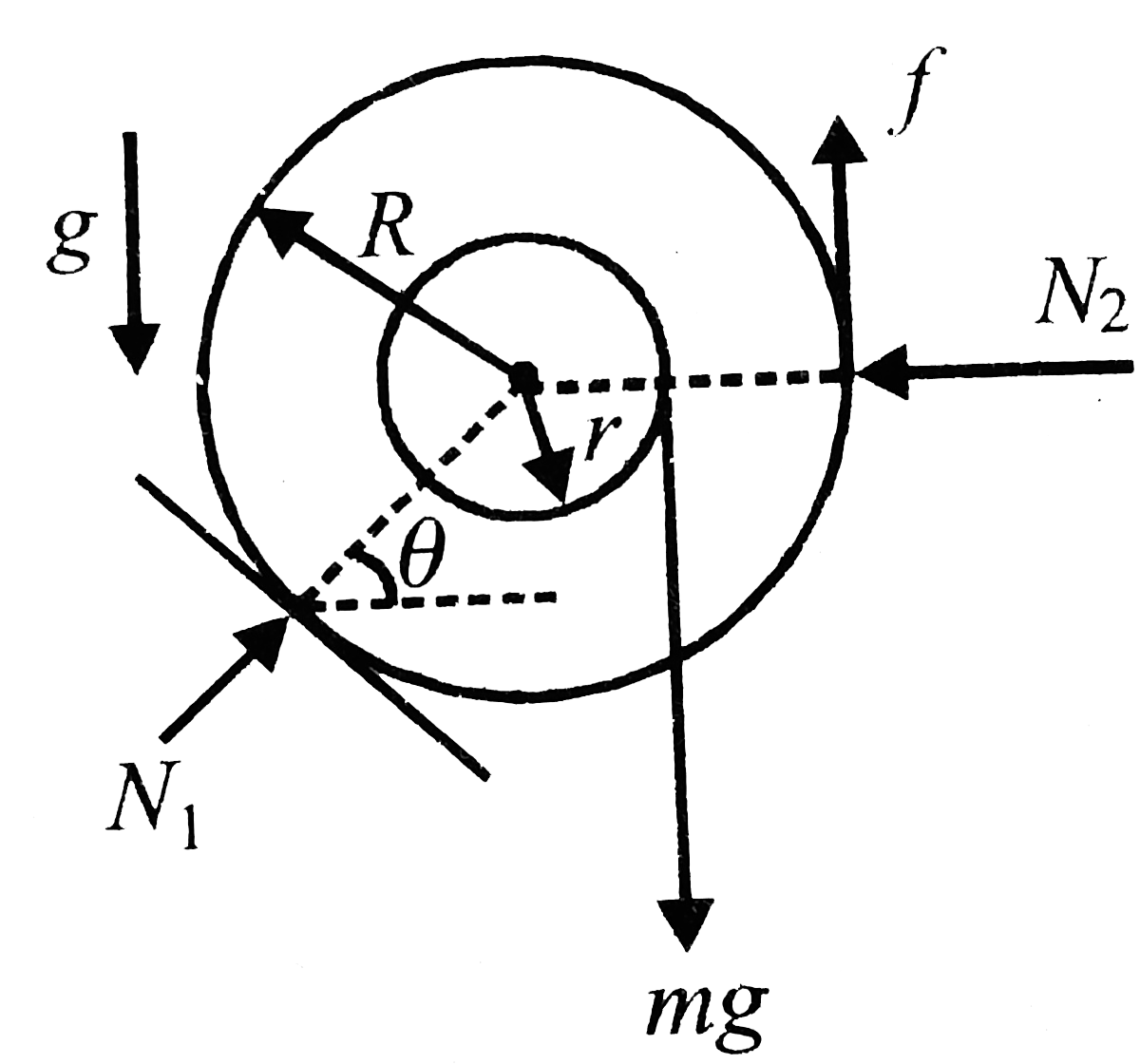
From eqn i. f=mgrR
From eqn ii and iii N2=mg−ftanθ=mgtanθ[1−rR]
Net force at B:fB=√f2+N22
For the minimum value of μ:f≤μN2
⇒mgrr≤μmgtanθ[1r/R]
⇒μ≥tanθR/r−1)
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
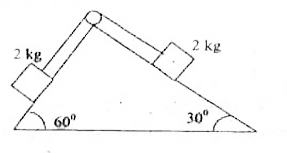
On the figure shown two blocks each of mass 2 kg are connected though a massless inextensible string, which posses over a frictionless pulley. The coefficient of friction between any two surface is μ=0.1. Find the acceleration of the blocks.
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View Solution
Knowledge Check
A massless spool of inner radius r, outer radius R is placed against vertical wall and tilted split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass m is hanging. There exists no friction at point A, while the coefficient of friction between spool and point B is μ . The angle between two surface is θ.
 AThe magnitude of force on the spool at B in order to maintain equilibrium is
AThe magnitude of force on the spool at B in order to maintain equilibrium is
mg√(rR)2+(1−rR)21tan2θBThe magnitude of force on the spool at B in order to maintain equilibrium is mg (1−rR)1tanθCThe minimum value of μ for the system to remain in equilibrium is cotθ(R−r)−1DThe minimum value of μ for the system to remain in equilibrium is tanθ(R−r)−1.A ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
Aθ=tan−1(μ)Bθ=tan−1(2μ)Cθ=tan−1(μ2)Dnone of theseA block of mass m=1kg has a speed v=4m/s at θ=60∘ on a circular track of radius R = 2 m as shown in figure. Size of the block is negligible. Coefficient of friction between block and the track is μ=0.5. The force of friction between the two is
 A10 NB8.5 NC6.5 ND5 N
A10 NB8.5 NC6.5 ND5 N
A mass of mass 60kg is pulling a mass M by an inextensible light rope passing through a smooth and massless pulley as shown in figure. The coefficient of friction between the mass and ground is μ=1/2 find the maximum value of M that can be pulled on the ground

View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
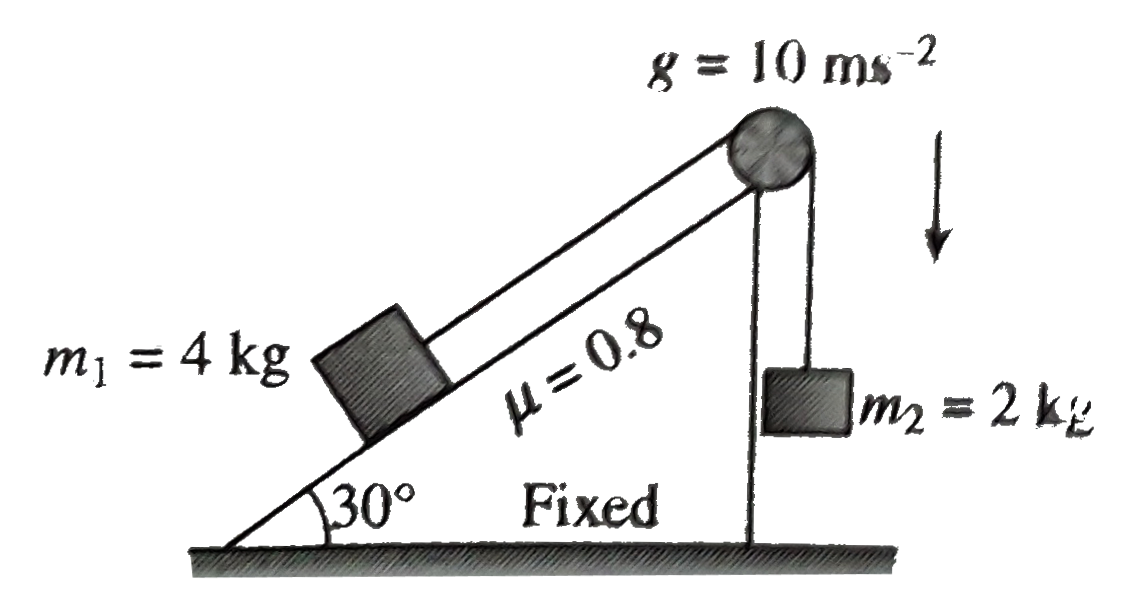
View SolutionTwo blocks of masses m1 and m2 are connected through a massless inextensible string .A block of mass m1 is placed at the fixed rigid inclined surface while the block of mass m2 hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m1 and m2 released from rest
View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View SolutionA spool of mass M and radius 2R lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. The value of m so that system is in equilibrium is
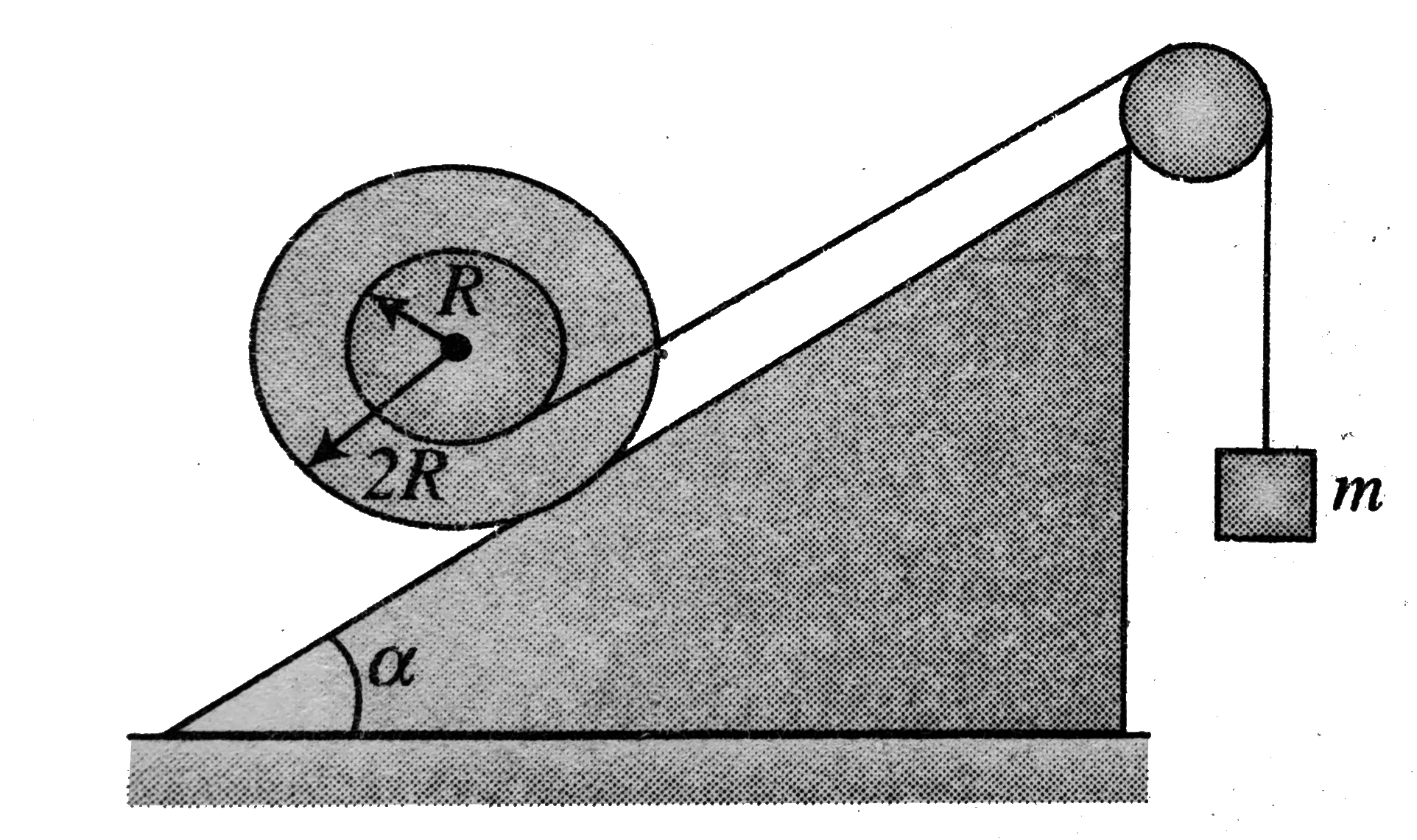
View Solution
