A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
ω0μR2g
ω0g2μR
2ω0Rμg
ω0R2μg
The correct Answer is:D
Taking τ about CM
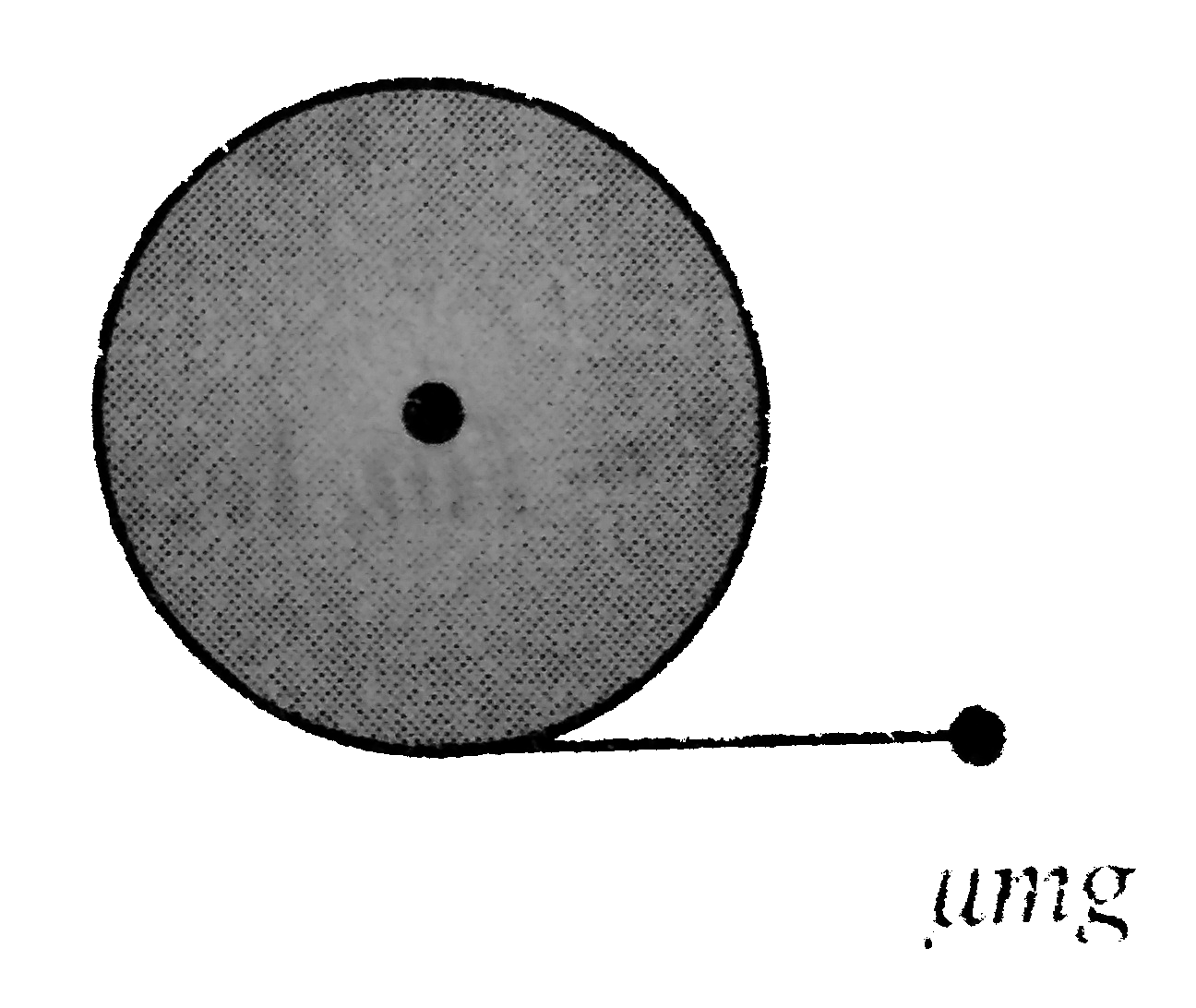
μmgR=MR2α
μg=Rα
α=μgR
ω=ω0=μgRf=ω02
ω02=μgRf⇒f=ω0R2μg
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be neglected as uniform.
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View Solution
Knowledge Check
A ring of radius R is first rotated withan angular velocity w, and then carefully placed on a rough horizontal surface. The coefficient of friction between the.surface and the ring is u. Time after which its angular speed is reduces to half is
A2ω0RμgBω0R2μgCω0μR2gDω0R2μRA uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μgA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
Aω0μkR2gBω0g2μkRC2ω0RμkgDω0R2μkg
A ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then :
View SolutionA solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
View SolutionA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
View SolutionA body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move

View SolutionA disc is given an initial angular velocity ω0 and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

View Solution
