A massless string passes around a frictionless pulley whose axis is horizontal. A monkey holds on to one end of the string and a body with the same mass as the monkey is attached to the other end. The monkey starts climbing upwards with an acceleration a. Then the other body moves
downward with an acceleration a
downward with a uniformly velocity
upward with an acceleration a
upward with an acceleration a/2
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on both the monkey and the body attached to the other end of the string.
1. Identify the masses and accelerations:
- Let the mass of the monkey be m.
- The mass of the body attached to the other end of the string is also m.
- The monkey is climbing upwards with an acceleration a.
2. Draw Free Body Diagrams (FBD):
- For the monkey:
- The forces acting on the monkey are the tension T in the string acting upwards and the weight mg acting downwards.
- For the body:
- The forces acting on the body are the tension T acting upwards and the weight mg acting downwards.
3. Apply Newton's Second Law for the monkey:
- For the monkey climbing upwards:
T−mg=ma
- Rearranging gives:
T=mg+ma(Equation 1)
4. Apply Newton's Second Law for the body:
- For the body moving downwards:
mg−T=ma′
- Here, a′ is the acceleration of the body. Rearranging gives:
T=mg−ma′(Equation 2)
5. Set the two expressions for tension equal:
- From Equation 1 and Equation 2:
mg+ma=mg−ma′
6. Solve for a′:
- Rearranging the equation gives:
ma′=−ma⟹a′=−a
- This indicates that the body moves downwards with the same magnitude of acceleration as the monkey climbs upwards.
7. Conclusion:
- Since the monkey climbs upwards with an acceleration a, the body moves downwards with an acceleration a.
Final Answer:
The body moves downwards with an acceleration a.
- Let the mass of the monkey be m.
- The mass of the body attached to the other end of the string is also m.
- The monkey is climbing upwards with an acceleration a.
- For the monkey:
- The forces acting on the monkey are the tension T in the string acting upwards and the weight mg acting downwards.
- For the body:
- The forces acting on the body are the tension T acting upwards and the weight mg acting downwards.
- For the monkey climbing upwards:
T−mg=ma
- Rearranging gives:
T=mg+ma(Equation 1)
- For the body moving downwards:
mg−T=ma′
- Here, a′ is the acceleration of the body. Rearranging gives:
T=mg−ma′(Equation 2)
- From Equation 1 and Equation 2:
mg+ma=mg−ma′
- Rearranging the equation gives:
ma′=−ma⟹a′=−a
- This indicates that the body moves downwards with the same magnitude of acceleration as the monkey climbs upwards.
- Since the monkey climbs upwards with an acceleration a, the body moves downwards with an acceleration a.
The body moves downwards with an acceleration a.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:MOTION IN A PLANE
Explore 87 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MAGNETISM AND MATTER )
Explore 52 Videos
- ATOMSBook:AAKASH SERIESChapter:ATOMSExercise:PRACTICE EXERCISE
Explore 21 Videos
Similar Questions
A massless string passes over a frictionless pulley and carries mass m1 hanging at one end and mass m2 connected by another massless string to mass m3 at other end as shown in figure. Calculate the tension in string joining masses m2andm3.
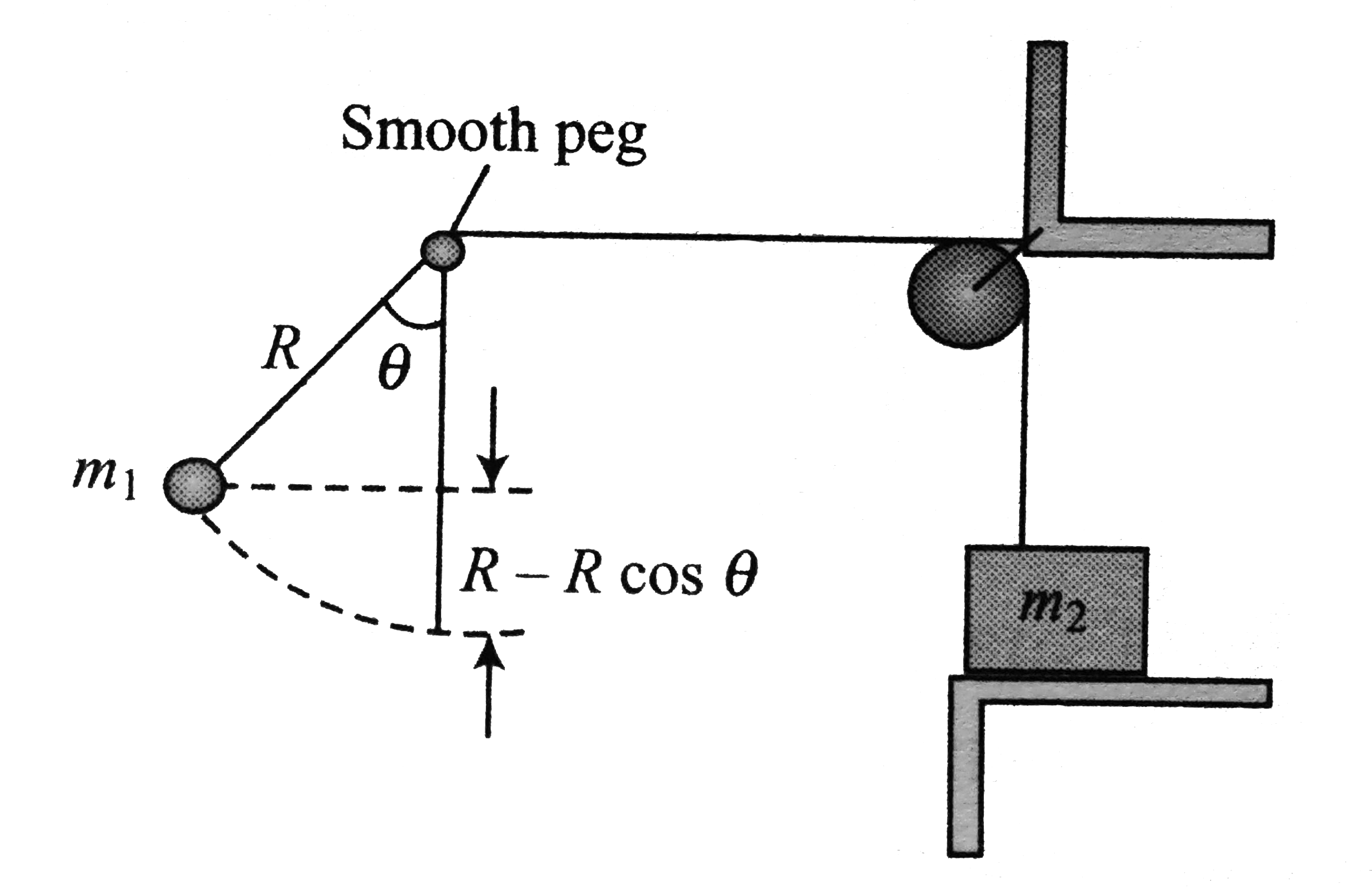
View SolutionTwo blocks are connected by a massless string that passes over a frictionless peg as shown in figure. One end of the string is attached to a mass m1=3kg, i.e., a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3−kg block be released in order to just lift the 6kg block off the table?
View Solution"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
View SolutionAs shown in figure a monkey of 20g mass is holding a light rope that passes over a frictionless pulley. A bunch of bananas of the same mass is tied to the other end of rope. Inorder to get access to the bunch the monkey starts climbing the rope. The distance between the monkey and the bananas is

View SolutionFigure shows a closed container completely filled with an ideal liquid of density ρ. In the liquid there is a spherical body of volume V and density σ attached to a string whose other end is attached to the roof of the container. The container is accelerating with an acceleration 'a' towards right. The force exerted by the liquid on the spherical body when it is in equillibrium with respect to the liquid, will be :
View SolutionA 20kg monkey has a firm hold on a light rope that passes over a frictionless pulley and is attached to a 20kg bunch of bananas. The monkey looks upwards , sees the bananas and starts to climb the rope to get them.
(a) As the monkey climbs ,do the bananas move up , move down or remain at rest?
(b) As the monkey climbs ,does the distance between the monkey and the banana decrease, increase or remain same?
(c) The monkey releases her hold on the rope .What happens to the distance between the monkey and the bananas while she is falling ?
(d) Before reaching the ground , the monkey grabs the rope to stop her fall. What will happen to bananas ?
View SolutionTwo ladders are hanging from ands of a light rope passing over a light and smooth pulley. A monkey of mass 2m hangs near the bottom of one ladder whose mass is M-2m. Another monkey of mass m hangs near the bottom of the other ladder whose mass is M-m. The monkey of mass 2m moves up a distance l with respect to the ladder. The monkey of mass m moves up a distance l/2 with respect to the ladder. The displacement of centre of mass of the system is kml4M. Find the value of k.

View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
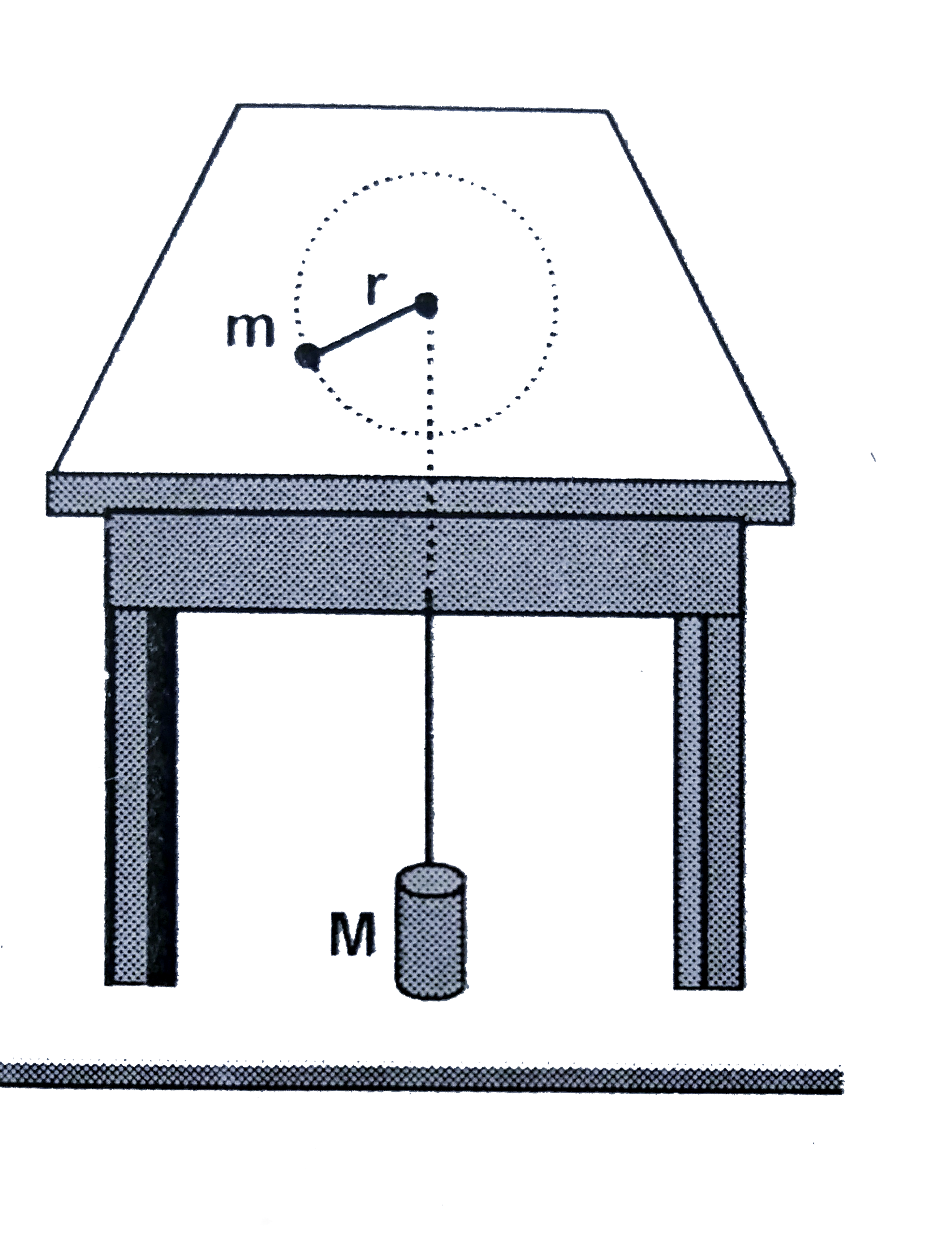
View SolutionA puck is moving in a circle in a circle of radius r0 with a constant speed v0 on a level frictionless table. A string is attached to the punk, which holds it in the circle, the string passes through a frictionless hole and is attached on the other end to a hanging object of mass M. The puck is mow made to move with a speed v'=3v0, but still in circle. The mass of the hanging object is left unchanged. The acceleration a' of the punk and the radius r' of the circle are now given by
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View Solution
