A massless string passes over a frictionless pulley and carries mass m1 hanging at one end and mass m2 connected by another massless string to mass m3 at other end as shown in figure. Calculate the tension in string joining masses m2andm3.
To solve the problem of finding the tension in the string joining masses m2 and m3, we will analyze the forces acting on each mass and apply Newton's second law of motion.
1. Identify the Forces:
- For mass m1 hanging, the forces are:
- Weight: m1g (downward)
- Tension T1 (upward)
- For mass m2:
- Weight: m2g (downward)
- Tension T1 (upward, from the string connected to m1)
- Tension T2 (downward, connected to m3)
- For mass m3:
- Weight: m3g (downward)
- Tension T2 (upward)
2. Write the Equations of Motion:
- For mass m1:
T1−m1g=−m1a(1)
- For mass m2:
m2g−T1−T2=m2a(2)
- For mass m3:
m3g−T2=m3a(3)
3. Solve for Acceleration a:
- Add equations (1), (2), and (3):
(T1−m1g)+(m2g−T1−T2)+(m3g−T2)=−m1a+m2a+m3a
Simplifying gives:
m2g+m3g−m1g−2T2=(m2+m3−m1)a
- Rearranging:
(m2+m3−m1)a=(m2+m3−m1)g⇒a=(m2+m3−m1)gm1+m2+m3
4. Substitute a into Equation for T2:
- From equation (3):
T2=m3g−m3a
- Substitute a:
T2=m3g−m3((m2+m3−m1)gm1+m2+m3)
- Simplifying:
T2=m3g(1−(m2+m3−m1)(m1+m2+m3))
- This can be further simplified to:
T2=m3(m1g)m1+m2+m3
Final Result:
The tension T2 in the string joining masses m2 and m3 is given by:
T2=m3m1gm1+m2+m3
- For mass m1 hanging, the forces are:
- Weight: m1g (downward)
- Tension T1 (upward)
- For mass m2:
- Weight: m2g (downward)
- Tension T1 (upward, from the string connected to m1)
- Tension T2 (downward, connected to m3)
- For mass m3:
- Weight: m3g (downward)
- Tension T2 (upward)
- For mass m1:
T1−m1g=−m1a(1)
- For mass m2:
m2g−T1−T2=m2a(2)
- For mass m3:
m3g−T2=m3a(3)
- Add equations (1), (2), and (3):
(T1−m1g)+(m2g−T1−T2)+(m3g−T2)=−m1a+m2a+m3a
Simplifying gives:
m2g+m3g−m1g−2T2=(m2+m3−m1)a
- Rearranging:
(m2+m3−m1)a=(m2+m3−m1)g⇒a=(m2+m3−m1)gm1+m2+m3
- From equation (3):
T2=m3g−m3a
- Substitute a:
T2=m3g−m3((m2+m3−m1)gm1+m2+m3)
- Simplifying:
T2=m3g(1−(m2+m3−m1)(m1+m2+m3))
- This can be further simplified to:
T2=m3(m1g)m1+m2+m3
The tension T2 in the string joining masses m2 and m3 is given by:
T2=m3m1gm1+m2+m3
Similar Questions
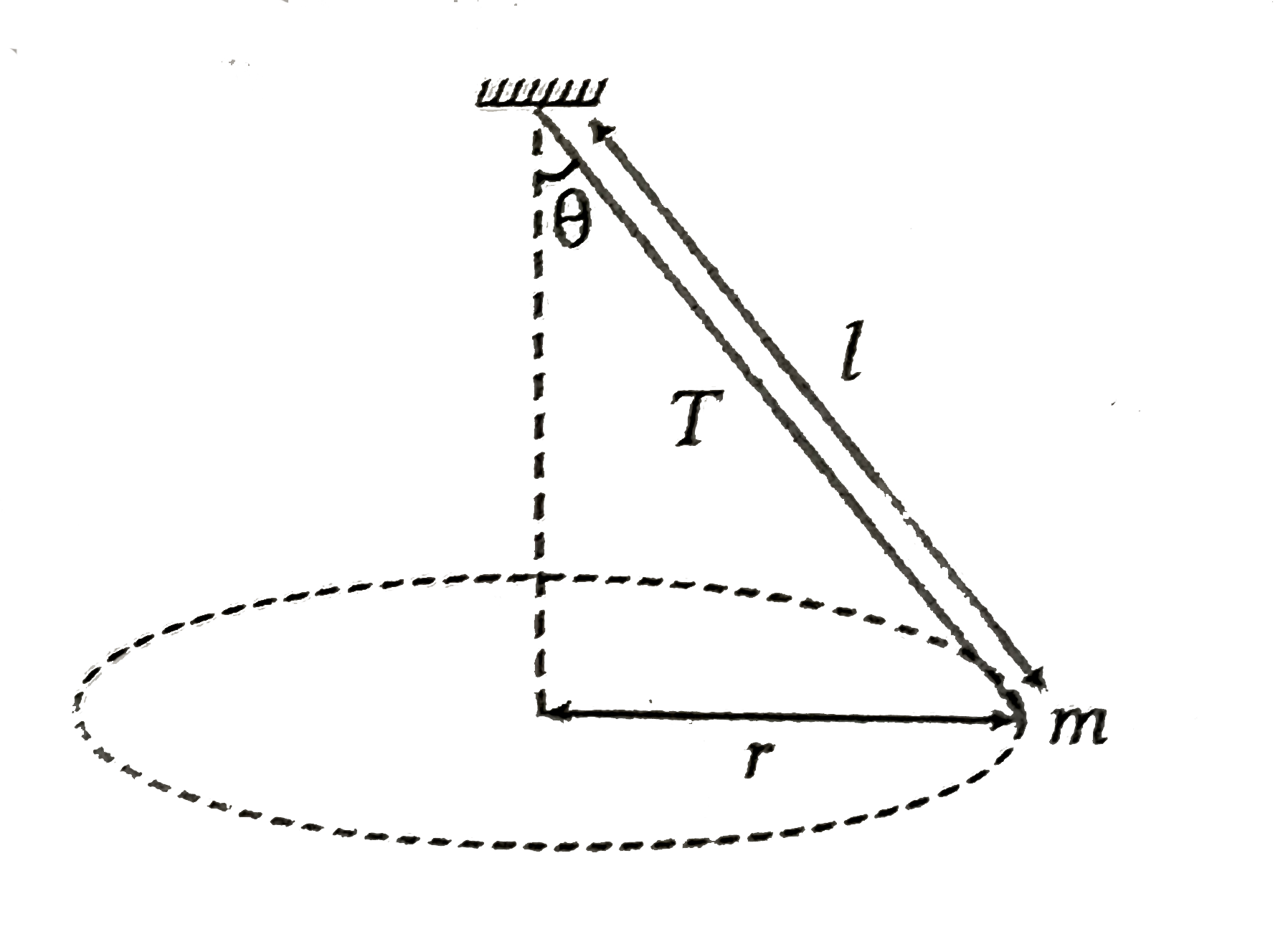
A string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
View SolutionA mass M is divided in two parts m and M−m. Now two parts are connected by an ideal string passing over a pulley as shown in diagram. Find value of m such that tension in string is maximum.
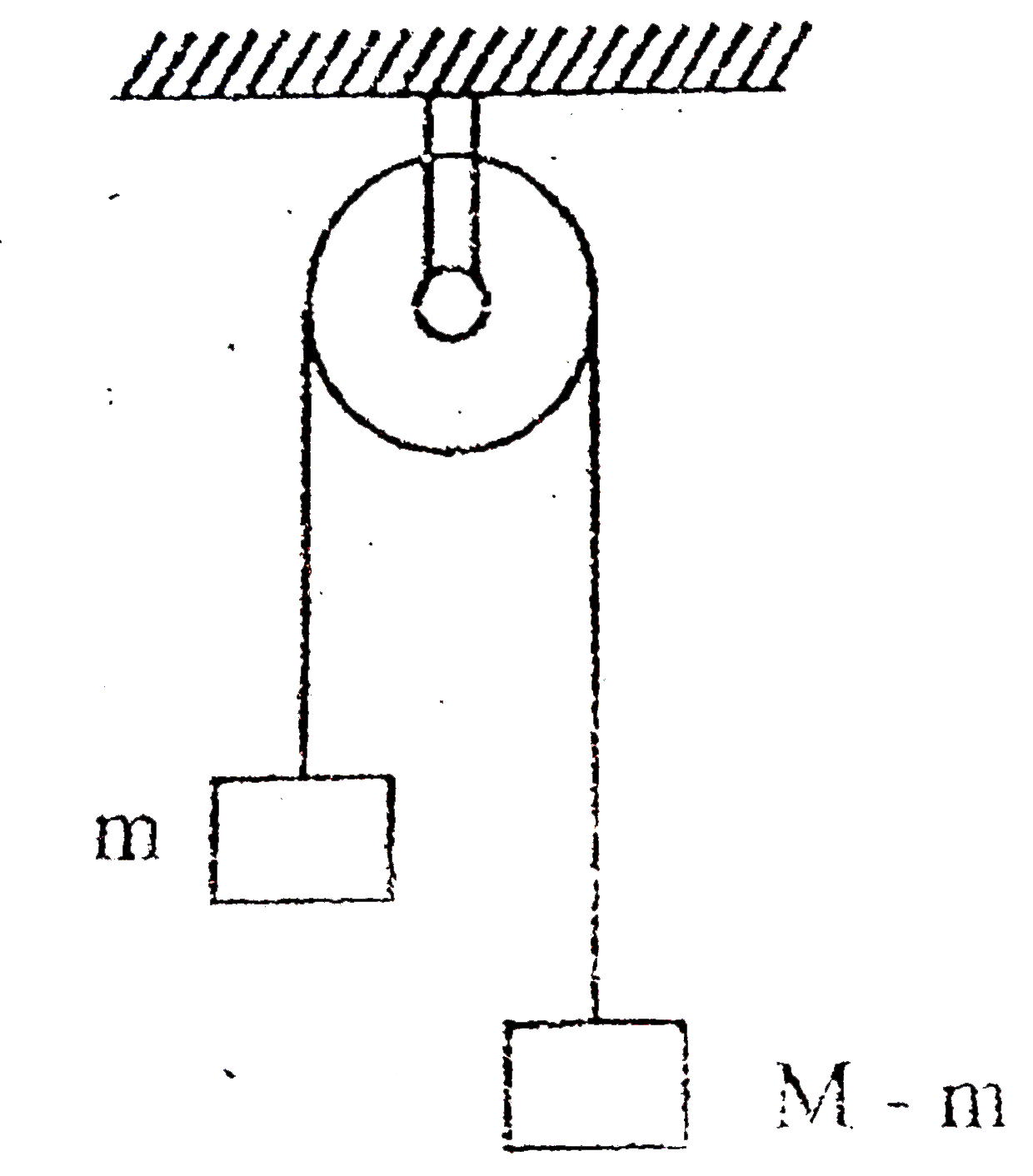
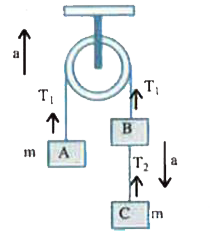
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in Fig. What are the tensions in the string connecting weights A to B and B to C?
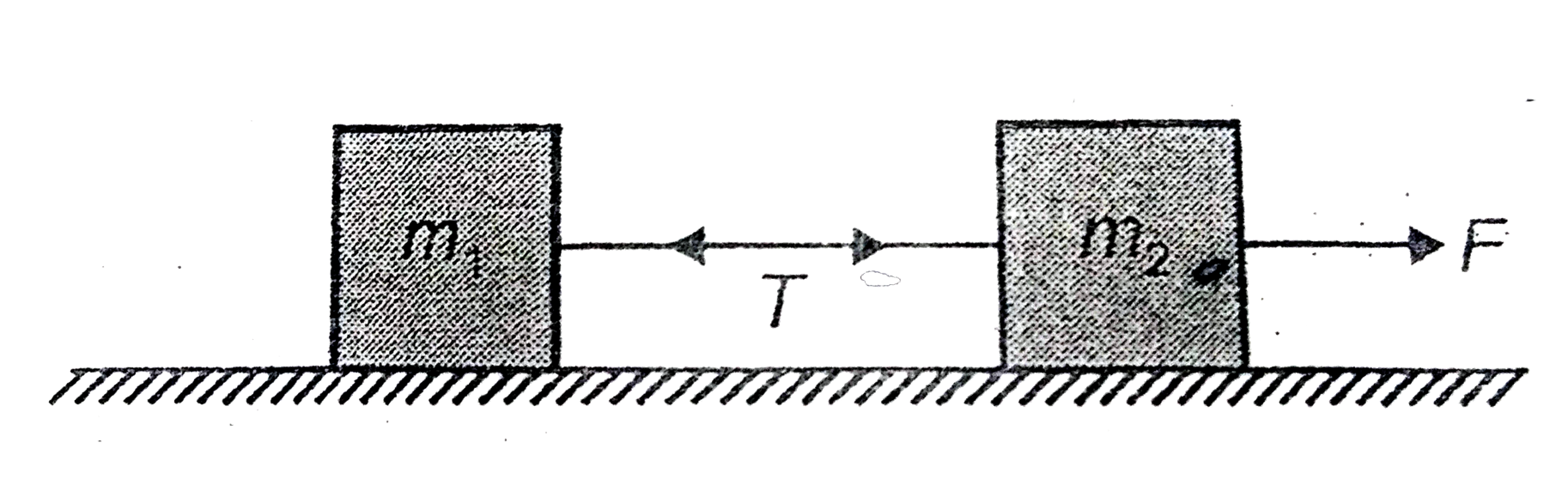
View SolutionTwo block of masses m1andm2 are lying on a frictionless horizontal table connected by a light string m2 is pulled by horizontal force F. Calculate the tension in the string .
View SolutionFigure shows three blocks of mass m each hanging on a string passing over a pulley. Calculate the tension in the string connecting A to B and B to C?

View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

View SolutionA block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
The tension in the string between masses m2andm3 is
View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
The tension in the string between masses m1andm2 is
View SolutionTwo blocks are connected by a massless string that passes over a frictionless peg as shown in figure. One end of the string is attached to a mass m1=3kg, i.e., a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3−kg block be released in order to just lift the 6kg block off the table?
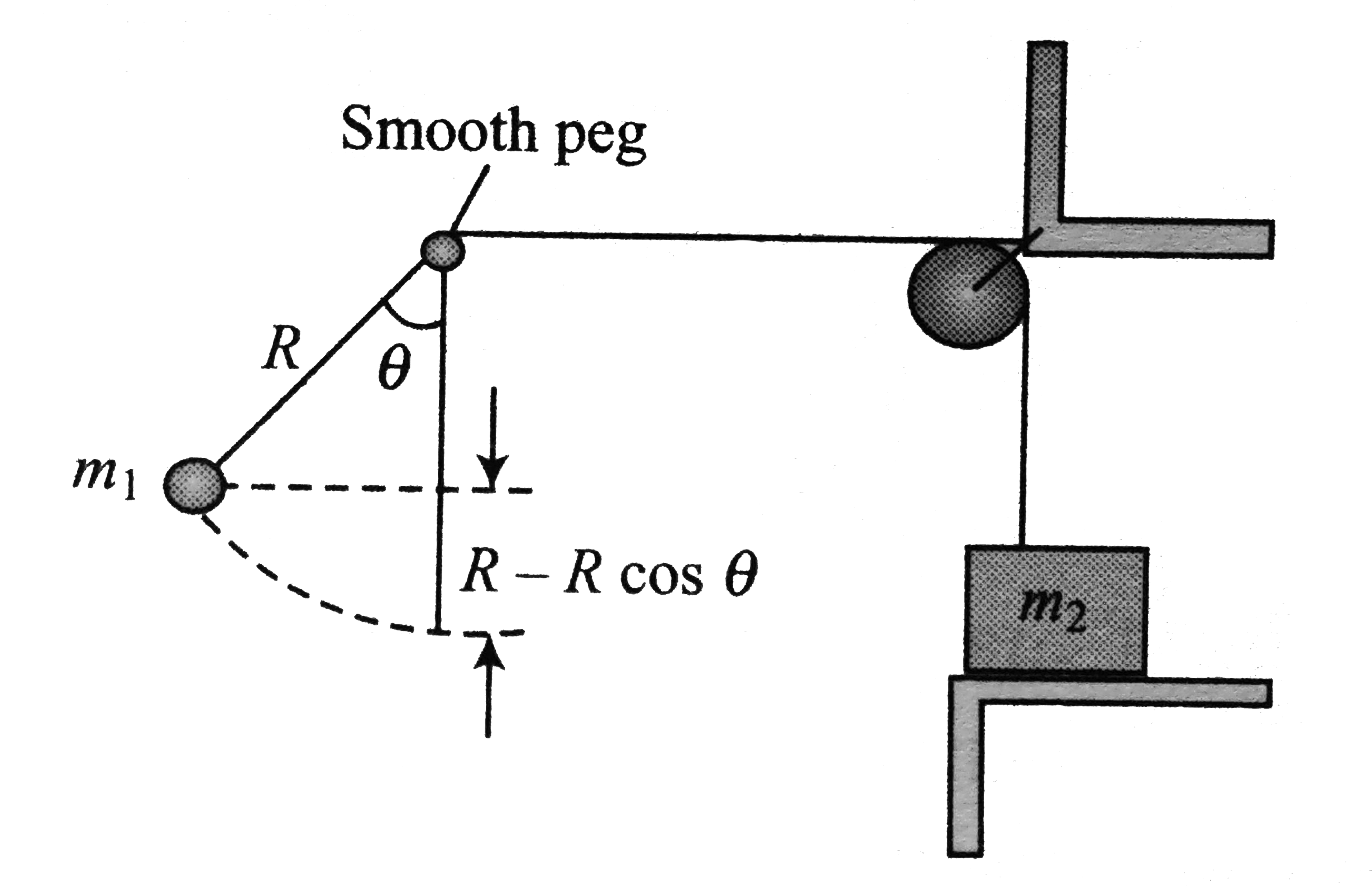
View Solution
