A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: $λ_{1} = 3650 A^{\circ}, λ_{2} = 4047 A^{\circ}, λ_{3} = 4358 A^{\circ}, λ_{4} = 5461 A^{\circ}, λ_{5} = 6907 A^{\circ}$ The stopping voltages, respectively were measured to be:
$V_{01} = 1.28 V, V_{02} = 0.95 V, V_{03} = 0.74 V, V_{04} = 0.16 V, V_{05} = 0 V$ .
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.

Video Solution

Text Solution

Verified by Experts

a. Let the respective frequencies fo the five spectral lines of mercury be $V_{1}, V_{2}, V_{3}, V_{4}$ and $V_{5}$ . Then
$V_{1} = \frac{c}{λ_{1}} = \frac{3 \times 10^{8}}{3650 \times 10^{- 1}} = 8.22 \times 10^{14} H z$
$V_{2} = \frac{c}{λ_{2}} = \frac{3 \times 10^{8}}{4047 \times 10^{- 10}} = 7.41 \times 10^{14} H z$
$V_{3} = \frac{c}{λ_{3}} = \frac{3 \times 10^{8}}{4358 \times 10^{- 10}} = 6.88 \times 10^{- 10} H z$
$V_{4} = \frac{c}{λ_{4}} = \frac{3 \times 10^{8}}{5461 \times 10^{- 10}} = 5.49 \times 10^{14} H z$
and $V_{5} = \frac{c}{λ_{5}} = \frac{3 \times 10^{8}}{5461 \times 10^{- 10}} = 4.34 \times 10^{14} H z$
From Einstein's photoelectric equation, we have
$h v = h v_{0} + \frac{1}{2} m v_{max}^{2}$
If $V_{0}$ is the stopping potential, then
$e V_{0} = \frac{1}{2} m v_{max}^{2}$
$h v = h v_{0} + e V_{0}$
or $V_{0} = \frac{h c}{e} - \frac{h v_{0}}{e}$
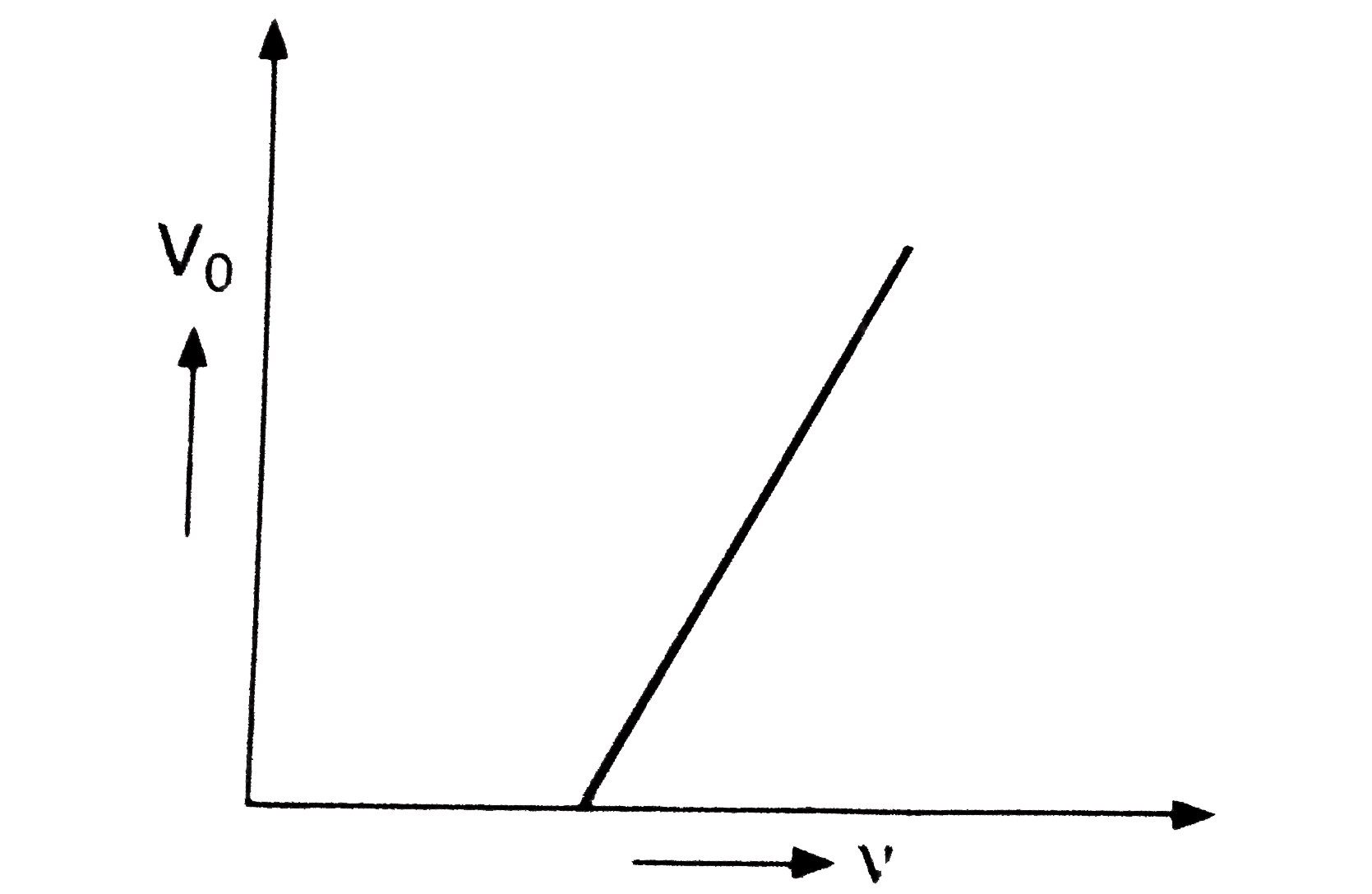
It represents the equation of a straight line, whose slope is $\frac{h}{e}$ and makes an intercept $\frac{h v_{0}}{e}$ on negative. $V_{0} - a ξ s$ . The plot of graph between v (along X-axis) and $V_{0}$ (along Y-axis) for the given data for the five spectral lines of mercury will be as shoen in fig

From the graph, slope of the graph is
$\frac{1.28 - 0.16}{8.22 \times 10^{14} - 5.49 \times 10^{14}} l = 4.1 \times 10^{- 15} J s C^{- 1}$
$\frac{h}{e} = 4.1 \times 10^{- 15}$
or $h = e \times 4.1 \times 10^{- 15}$
$= 1.6 \times 10^{- 19} \times 4.1 \times 10^{- 15}$
$= 6.57 \times 10^{- 34} J s$
b. Also the intercept made by the graph on v-axis is equal to $v_{0}$ . Therefore, from the graph, we have
$v_{0} = 5.15 \times 10^{14} H z$
Hence, the work function of rubidum,
$w = h v_{0}$
$= 6.456 \times 10^{34} \times 5.15 \times 10^{14}$
$= 3.38 \times 10^{- 19} J = \frac{3.38 \times 10^{- 19}}{1.6 \times 10^{- 19}} = 2.11 e V$

A photon of frequency $v$ causes photo electric emission from a surface with threshold frequency $v_{0}$ . The de-Broglies wavelength $(λ)$ of the photo electron emitted is given by:
A $Δ n = \frac{h}{2 m λ}$
B $Δ n = \frac{h}{λ}$
C $[\frac{1}{v_{0}} - \frac{1}{v}] = \frac{m c^{2}}{h}$
D $λ = \sqrt{\frac{h}{2 m Δ V}}$
If $λ_{v}, λ_{m} and λ_{x}$ represent wavlength of visible light, microwaves and X - rays respectively, then
A $λ_{m} < λ_{x} < λ_{v}$
B $λ_{v} < λ_{m} < λ_{x}$
C $λ_{x} < λ_{v} < λ_{m}$
D $λ_{m} < λ_{v} < λ_{x}$
if $λ_{v'}, λ_{x}$ and $λ_{m}$ represent the wavelengths of visible light X-rays and microwaves respectively then:
A $λ_{m} > λ_{x} > λ_{v}$
B $λ_{k} > λ_{m} > λ_{x}$
C $λ_{m} > λ_{v} > λ_{x}$
D $λ_{y} > λ_{x} > λ_{m}$