A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red and end of the visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used:
$λ_{1} = 3650 Å, λ_{2} = 4047 Å, λ_{3} = 4358 Å, λ_{4} = 5461 Å, λ_{5} = 6907 Å$
The stopping voltages, respectively, were measured to be:
$V_{01} = 1.28 V, V_{02} = 0.95 V, V_{03} = 0.74 V, V_{04} = 0.16 V, V_{05} = 0 V$
Determine the value of Planck's constant h, the threshold frequency and work function for the material.

Text Solution

Verified by Experts

Frequencies corresponding to different wavelengths of spectral lines of mercury are
$v_{1} = \frac{c}{λ_{1}} = \frac{3 \times 10^{8}}{3650 \times 10^{- 10}} = 8.219 \times 10^{14} H z$

$v_{2} = \frac{c}{λ_{2}} = \frac{3 \times 10^{8}}{4047 \times 10^{- 10}} = 7.412 \times 10^{14} H z$
$v_{3} = \frac{c}{λ_{3}} = \frac{3 \times 10^{8}}{4358 \times 10^{- 10}} = 6.883 \times 10^{14} H z$
$v_{4} = \frac{c}{λ_{4}} = \frac{3 \times 10^{8}}{5461 \times 10^{- 10}} = 5.493 \times 10^{14} H z$
and $v_{5} = \frac{c}{λ_{5}} = \frac{3 \times 10^{8}}{6907 \times 10^{- 10}} = 4.343 \times 10^{14} H z$
From the given data, we plot the graph, which comes out to be as shown in figure. first four points lie on a straight line but the fifth point does not lie on straight line. it means that $v_{5} < v_{0}$ .
(a) A careful measurement shows that slope of straight line graph is $4.15 \times 10^{- 15} V s$
$∴ \frac{h}{e} = 4.15 \times 10^{- 15} = e \times 4.15 \times 10^{- 15} = 1.6 \times 10^{- 19} \times 4.15 \times 10^{- 15} = 6.64 \times 10^{- 34} J s$
(b) From graph intercept along v-axis is found to be $5 \times 10^{14} H z$ .
$∴$ Threshold frequency $v_{0} = 5 \times 10^{14} H z$
$∴$ Work function $ϕ_{0} = 6.64 \times 10^{- 34} \times 5 \times 10^{14} J = \frac{6.64 \times 10^{- 34} \times 5 \times 10^{14}}{1.6 \times 10^{- 19}} e V$
$= 2.075 e V = 2.1 e V$ .

Updated on:21/07/2023

The dependence of the short wavelength limit $λ_{min}$ on the accelerating potential $V$ is represented by the curve of figure

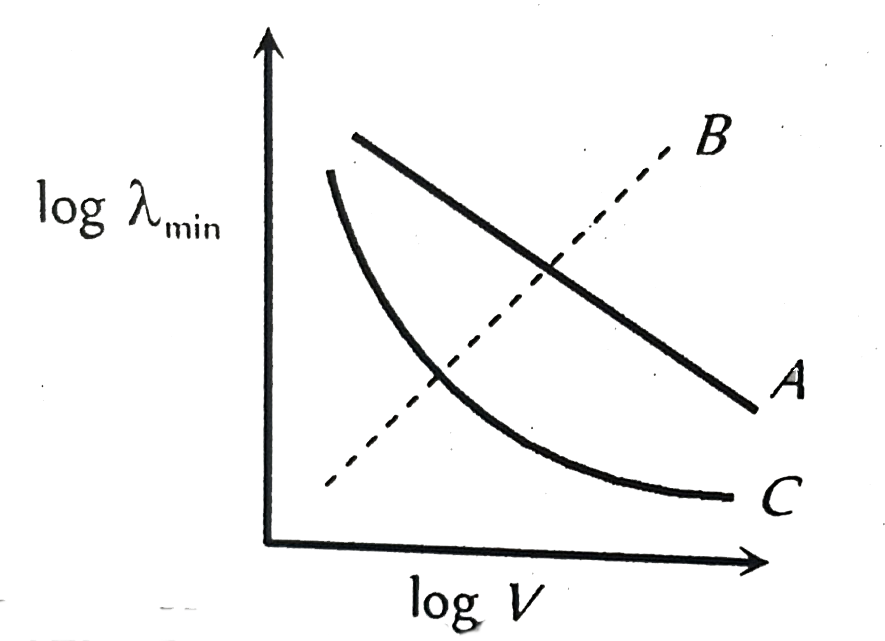AA
BB
CC
DNone of these
X-rays of $λ = 1 Å$ have frequency
A $3 \times 10^{8} H z$
B $3 \times 10^{18} H z$
C $3 \times 10^{10} H z$
D $3 \times 10^{15} H z$
The ration of resolving powers of an optical microscope for two wavelangths
$λ_{1} = 4000$ $Å and λ_{2} = 6000 Å i s$
A $8 : 27$
B $9 : 4$
C $3 : 2$
D $16 : 81$