A Merry -go-round, made of a ring-like plarfrom of radius RandmassM, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially awaay from the centre of the round (as see from the round). The speed of the round after wards is
2ω
ω
ω2
0
The correct Answer is:A
To solve the problem, we need to apply the principle of conservation of angular momentum. Here's a step-by-step solution:
Step 1: Understand the System
We have a merry-go-round (ring-like platform) with mass M and radius R that is rotating with an angular speed ω. A person of mass m is standing on the edge of the merry-go-round.
Step 2: Define Initial Angular Momentum
Before the person jumps off, the total angular momentum Linitial of the system (merry-go-round + person) can be calculated as follows:
- The angular momentum of the merry-go-round is given by:
Lmerry-go-round=Imerry-go-round⋅ω=MR2⋅ω
- The angular momentum of the person (considered as a point mass at a distance R from the center) is:
Lperson=mR2⋅ω
- Therefore, the total initial angular momentum is:
Linitial=Lmerry-go-round+Lperson=(M+m)R2ω
Step 3: Define Final Angular Momentum
After the person jumps off, they move radially away from the center. The angular momentum of the merry-go-round after the jump (with the person no longer on it) is:
- The angular momentum of the merry-go-round becomes:
Lfinal=MR2⋅ω′
where ω′ is the new angular speed of the merry-go-round after the person jumps off.
Step 4: Apply Conservation of Angular Momentum
According to the conservation of angular momentum:
Linitial=Lfinal
Substituting the expressions we derived:
(M+m)R2ω=MR2⋅ω′
Step 5: Solve for the New Angular Speed
We can simplify this equation by canceling R2 from both sides:
(M+m)ω=Mω′
Now, solving for ω′:
ω′=(M+m)ωM
Step 6: Substitute the Mass of the Person
In this case, since the mass of the person is also M:
ω′=(M+M)ωM=2MωM=2ω
Conclusion
The speed of the merry-go-round after the person jumps off is:
ω′=2ω
We have a merry-go-round (ring-like platform) with mass M and radius R that is rotating with an angular speed ω. A person of mass m is standing on the edge of the merry-go-round.
Before the person jumps off, the total angular momentum Linitial of the system (merry-go-round + person) can be calculated as follows:
- The angular momentum of the merry-go-round is given by:
Lmerry-go-round=Imerry-go-round⋅ω=MR2⋅ω
- The angular momentum of the person (considered as a point mass at a distance R from the center) is:
Lperson=mR2⋅ω
- Therefore, the total initial angular momentum is:
Linitial=Lmerry-go-round+Lperson=(M+m)R2ω
After the person jumps off, they move radially away from the center. The angular momentum of the merry-go-round after the jump (with the person no longer on it) is:
- The angular momentum of the merry-go-round becomes:
Lfinal=MR2⋅ω′
where ω′ is the new angular speed of the merry-go-round after the person jumps off.
According to the conservation of angular momentum:
Linitial=Lfinal
Substituting the expressions we derived:
(M+m)R2ω=MR2⋅ω′
We can simplify this equation by canceling R2 from both sides:
(M+m)ω=Mω′
Now, solving for ω′:
ω′=(M+m)ωM
In this case, since the mass of the person is also M:
ω′=(M+M)ωM=2MωM=2ω
The speed of the merry-go-round after the person jumps off is:
ω′=2ω
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionConsidering a body of mass m, radius R rotating with angular speed ω about the centre of the mass and with a velocity v of centre of mass, the most appropriate definition of rolling motion will be
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with an angular speed ω0 two particles each of mass m are now attached at diametrically opposite points. Find new angular speed of the ring.
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become
View SolutionA uniform brass disc of radius a and mass m is set into spinning with angular speed ω0 about an axis passing through centre of disc and perpendicular to the palne of disc. If its temperature increases from θ∘1C to θ∘2C with out disturbing the disc, what will be its new angular speed ?
View SolutionA satellite of mass m is in a circular orbit of radius r round the Earth. Calculate its angular momentum with respect to the centre of the orbit in terms of the mass M of the Earth and G.
View SolutionA cord is wound round the circumference of a solid cylinder radius R and mass M. The axis of the cylinder is horizontal. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h.

If the mass starts from rest and falls a distance h, then its speed at that instant is:
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
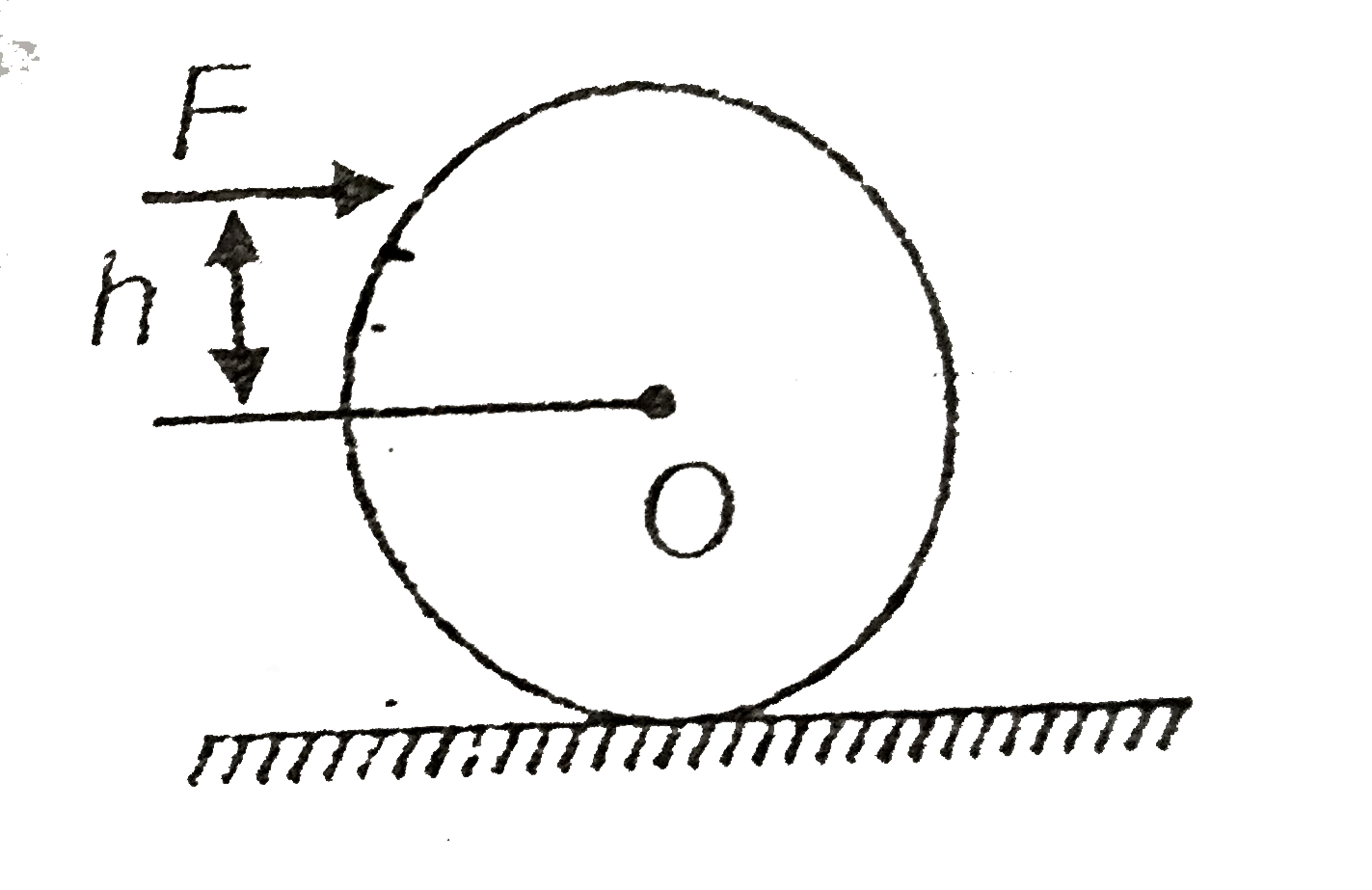
View Solution
