Considering a body of mass m, radius R rotating with angular speed ω about the centre of the mass and with a velocity v of centre of mass, the most appropriate definition of rolling motion will be
v = R ω
the point of contact is stationary
the point of contact is stationary with respect to the surface
the body purely rotates about the point of contact
The correct Answer is:C
To solve the problem regarding the definition of rolling motion for a body of mass m, radius R, rotating with angular speed ω about its center of mass and having a velocity v of its center of mass, we will follow these steps:
1. Understanding Rolling Motion:
- Rolling motion occurs when a body rolls over a surface without slipping. For pure rolling motion, the point of contact between the body and the surface must have zero velocity relative to the surface.
2. Identifying Key Parameters:
- Let the radius of the body be R.
- The angular speed of the body is ω.
- The translational velocity of the center of mass is v.
3. Velocity of the Point of Contact:
- The velocity of the center of mass v is directed along the positive x-axis.
- The point of contact (let's call it point P) will have a velocity due to the rotation of the body. This velocity can be expressed as Rω and will be directed opposite to the direction of the translational motion (i.e., in the negative x-direction).
4. Condition for Pure Rolling Motion:
- For pure rolling motion, the velocity of the point of contact with respect to the surface must be zero. Therefore, we can set up the equation:
v−Rω=0
- Rearranging gives us:
v=Rω
5. Conclusion:
- The condition v=Rω indicates that the body is rolling without slipping, meaning the point of contact is stationary with respect to the surface. Thus, the most appropriate definition of rolling motion is that the point of contact is stationary with respect to the surface.
Final Answer:
The most appropriate definition of rolling motion is that the point of contact is stationary with respect to the surface, which corresponds to the condition v=Rω.
---
- Rolling motion occurs when a body rolls over a surface without slipping. For pure rolling motion, the point of contact between the body and the surface must have zero velocity relative to the surface.
- Let the radius of the body be R.
- The angular speed of the body is ω.
- The translational velocity of the center of mass is v.
- The velocity of the center of mass v is directed along the positive x-axis.
- The point of contact (let's call it point P) will have a velocity due to the rotation of the body. This velocity can be expressed as Rω and will be directed opposite to the direction of the translational motion (i.e., in the negative x-direction).
- For pure rolling motion, the velocity of the point of contact with respect to the surface must be zero. Therefore, we can set up the equation:
v−Rω=0
- Rearranging gives us:
v=Rω
- The condition v=Rω indicates that the body is rolling without slipping, meaning the point of contact is stationary with respect to the surface. Thus, the most appropriate definition of rolling motion is that the point of contact is stationary with respect to the surface.
The most appropriate definition of rolling motion is that the point of contact is stationary with respect to the surface, which corresponds to the condition v=Rω.
Similar Questions
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move

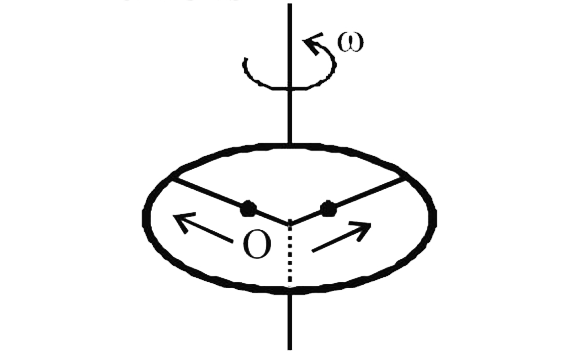
View SolutionA ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is 89ω and one fo the masses is at a distance of 35R from O. At this instant the distance of the other mass from O is
View SolutionA solid sphere of mass M and radius R is in pure rolling as shown in figure. The angular momentum of the sphere about the origin is (linear velocity of centre of mass is v0, in positive x-direction)
View Solution