A metal rod of 30 cm length expands by 0.075 cm when its temperature is raised from 0∘C to 100∘C. Another rod of a different metal of length 45 cm expands by 0.045 cm for the same rise in temperature. A composite rod C made by joining A and B end to end expands by 0.040 cm when its length is 45 cm and it is heated from 0∘C to 50∘C. Find the length of each portion of the composite rod.
To solve the problem step by step, we will first determine the coefficients of linear expansion for each rod, and then we will use these values to find the lengths of the portions of the composite rod.
Step 1: Calculate the coefficient of linear expansion for rod A
Given:
- Length of rod A, LA=30cm
- Expansion of rod A, ΔLA=0.075cm
- Temperature change, ΔT=100−0=100°C
Using the formula for linear expansion:
ΔLA=αA⋅LA⋅ΔT
Rearranging to find αA:
αA=ΔLALA⋅ΔT=0.07530⋅100
Calculating αA:
αA=0.0753000=25×10−6per °C
Step 2: Calculate the coefficient of linear expansion for rod B
Given:
- Length of rod B, LB=45cm
- Expansion of rod B, ΔLB=0.045cm
Using the same formula:
ΔLB=αB⋅LB⋅ΔT
Rearranging to find αB:
αB=ΔLBLB⋅ΔT=0.04545⋅100
Calculating αB:
αB=0.0454500=10×10−6per °C
Step 3: Set up the equation for the composite rod C
Let:
- L′A = length of rod A in composite rod C
- L′B = length of rod B in composite rod C
We know:
L′A+L′B=45cm
Step 4: Calculate the total expansion of the composite rod C
Given:
- Expansion of composite rod C, ΔLC=0.040cm
- Temperature change for composite rod C, ΔT=50−0=50°C
Using the expansion formula:
ΔLC=ΔL′A+ΔL′B
Substituting the expansions:
ΔL′A=αA⋅L′A⋅ΔT
ΔL′B=αB⋅L′B⋅ΔT
Thus:
0.040=αA⋅L′A⋅50+αB⋅L′B⋅50
Substituting the values of αA and αB:
0.040=(25×10−6)⋅L′A⋅50+(10×10−6)⋅L′B⋅50
Simplifying:
0.040=(1.25×10−3)L′A+(0.5×10−3)L′B
Step 5: Substitute L′B in terms of L′A
From L′A+L′B=45:
L′B=45−L′A
Substituting into the expansion equation:
0.040=(1.25×10−3)L′A+(0.5×10−3)(45−L′A)
Expanding:
0.040=(1.25×10−3)L′A+(22.5×10−3)−(0.5×10−3)L′A
Combining like terms:
0.040=(0.75×10−3)L′A+22.5×10−3
Rearranging:
(0.75×10−3)L′A=0.040−22.5×10−3
Calculating:
(0.75×10−3)L′A=0.040−0.0225=0.0175
Solving for L′A:
L′A=0.01750.75×10−3≈23.33cm
Step 6: Calculate L′B
Using L′B=45−L′A:
L′B=45−23.33≈21.67cm
Final Answer
- Length of rod A in composite rod C: L′A≈23.33cm
- Length of rod B in composite rod C: L′B≈21.67cm
- Length of rod A, LA=30cm
- Expansion of rod A, ΔLA=0.075cm
- Temperature change, ΔT=100−0=100°C
ΔLA=αA⋅LA⋅ΔT
Rearranging to find αA:
αA=ΔLALA⋅ΔT=0.07530⋅100
Calculating αA:
αA=0.0753000=25×10−6per °C
- Length of rod B, LB=45cm
- Expansion of rod B, ΔLB=0.045cm
ΔLB=αB⋅LB⋅ΔT
Rearranging to find αB:
αB=ΔLBLB⋅ΔT=0.04545⋅100
Calculating αB:
αB=0.0454500=10×10−6per °C
- L′A = length of rod A in composite rod C
- L′B = length of rod B in composite rod C
L′A+L′B=45cm
- Expansion of composite rod C, ΔLC=0.040cm
- Temperature change for composite rod C, ΔT=50−0=50°C
ΔLC=ΔL′A+ΔL′B
Substituting the expansions:
ΔL′A=αA⋅L′A⋅ΔT
ΔL′B=αB⋅L′B⋅ΔT
Thus:
0.040=αA⋅L′A⋅50+αB⋅L′B⋅50
Substituting the values of αA and αB:
0.040=(25×10−6)⋅L′A⋅50+(10×10−6)⋅L′B⋅50
Simplifying:
0.040=(1.25×10−3)L′A+(0.5×10−3)L′B
L′B=45−L′A
Substituting into the expansion equation:
0.040=(1.25×10−3)L′A+(0.5×10−3)(45−L′A)
Expanding:
0.040=(1.25×10−3)L′A+(22.5×10−3)−(0.5×10−3)L′A
Combining like terms:
0.040=(0.75×10−3)L′A+22.5×10−3
Rearranging:
(0.75×10−3)L′A=0.040−22.5×10−3
Calculating:
(0.75×10−3)L′A=0.040−0.0225=0.0175
Solving for L′A:
L′A=0.01750.75×10−3≈23.33cm
L′B=45−23.33≈21.67cm
- Length of rod A in composite rod C: L′A≈23.33cm
- Length of rod B in composite rod C: L′B≈21.67cm
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.3
18 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.1
23 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A metal rod (A) of 25cm length expands by 0.050cm when its temperature is raised from 0∘C to 100∘C. Another rod (B) of a different metal of length 40cm expamds by 0.040cm for the same rise in temperature. A third rod ( C) of 50cm length is made up of pieces of rods (A) and (B) placed end to end expands by 0.03cm on heating from 0∘C. Find the lengths of each portion of the composite rod.
View SolutionA metal rod A of length l0 expands by Δl when its temperature is raised by 100∘C. Another rod B of different metal of length 2l0 expands by Δl/2 for same rise in temperature. A third rod C of length 3l0 is made up of pieces of rods A and B placed end to end expands by 2Δl on heating through 100K . The length of each portion of the composite rod is :-
View SolutionA rod of length 20 cm made of metal A expands by 0.075 when its temperature is raised from 0∘C to 100∘C. Another rod of a different metal B having the same length expands by 0.045 cm for the same change in temperature. A third rod of the same length is composed of two parts, one of metal A and other of metal B. This rod expands by 0.065 cm for the same change in temperature. The portion made of metal A has the length :
View SolutionAn aluminium rod of length 50cm is heated so that its temperature increases from 20∘C to 80∘C. If the linear coefficient of expansion of aluminium is 24×10−6/∘C find the increase in the length of the aluminium rod.
View SolutionOn heating the metal rod of length 2m from 0°C to 50°C, its length is increased by 0.1 cm. the coeffecient of linear expansion of metal rod is
View SolutionTwo rods of equal cross sections, one of copper and the other of steel, are joined to form a composite rod of length 2.0 m at 20∘C, the length of the copper rod is 0.5 m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the lengths of the component rods also do not change with increase in temperature. Calculate Young's moulus of steel. (The coefficient of linear expansion of copper, αc=1.6×10−5∘C and Young's modulus of copper is 1.3×1013N/m2).
View SolutionThe length of a cylinder is measured with a meter rod having least count 0.1cm. Its diameter is measured with Vernier calipers having least count 0.01cm. Given that length is 5.0cm and radius is 2cm. Find the percentage error in the calculated value of the volume.
View SolutionThe temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
View SolutionThree rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
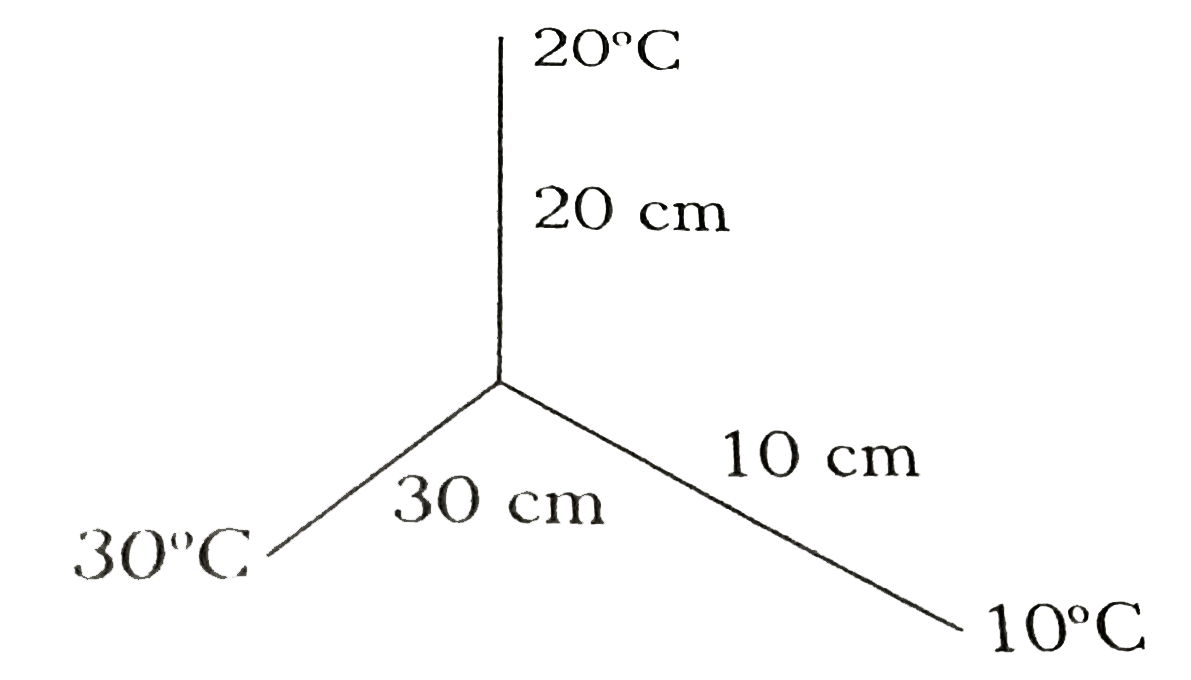
View SolutionA rod of certain metal is 1.0m long and 0.6cm in diameter. Its resistance is 3.0×10&(−3) ohm. Another disc made of the same metal is 2.0cm in diameter and 1.0mm thick. What is the resistance between the round faces of the disc?
View Solution
