A rod of certain metal is 1.0m long and 0.6cm in diameter. Its resistance is 3.0×10&(−3) ohm. Another disc made of the same metal is 2.0cm in diameter and 1.0mm thick. What is the resistance between the round faces of the disc?
1.35×10−4Ω
2.70×10−7Ω
4.05×10−6Ω
8.10×10−5Ω
To solve the problem step by step, we will first calculate the resistivity of the metal using the given dimensions and resistance of the rod, and then use that resistivity to find the resistance of the disc.
Step 1: Calculate the area of the rod
The area A of the rod can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the rod. The diameter of the rod is given as 0.6cm, so the radius r is:
r=0.6cm2=0.3cm=0.3×10−2m=0.003m
Now, substituting the radius into the area formula:
A=π(0.003)2=π×9×10−6m2=2.827×10−5m2
Step 2: Calculate the resistivity of the metal
Using the formula for resistance:
R=ρLA
we can rearrange it to find the resistivity ρ:
ρ=R⋅AL
Substituting the values:
- R=3.0×10−3Ω
- A=2.827×10−5m2
- L=1.0m
Calculating ρ:
ρ=3.0×10−3×2.827×10−51.0=8.481×10−8Ω⋅m
Step 3: Calculate the area of the disc
The area Ad of the disc can also be calculated using the formula for the area of a circle:
Ad=πr2d
where rd is the radius of the disc. The diameter of the disc is given as 2.0cm, so the radius rd is:
rd=2.0cm2=1.0cm=1.0×10−2m
Now, substituting the radius into the area formula:
Ad=π(0.01)2=π×1×10−4m2=3.142×10−4m2
Step 4: Calculate the resistance of the disc
Now we can calculate the resistance Rd of the disc using the formula:
Rd=ρLdAd
where Ld is the thickness of the disc, which is 1.0mm=1.0×10−3m.
Substituting the values:
Rd=8.481×10−8×1.0×10−33.142×10−4
Calculating Rd:
Rd=8.481×10−113.142×10−4≈2.70×10−7Ω
Final Answer
The resistance between the round faces of the disc is approximately 2.7×10−7Ω.
---
The area A of the rod can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the rod. The diameter of the rod is given as 0.6cm, so the radius r is:
r=0.6cm2=0.3cm=0.3×10−2m=0.003m
Now, substituting the radius into the area formula:
A=π(0.003)2=π×9×10−6m2=2.827×10−5m2
Using the formula for resistance:
R=ρLA
we can rearrange it to find the resistivity ρ:
ρ=R⋅AL
Substituting the values:
- R=3.0×10−3Ω
- A=2.827×10−5m2
- L=1.0m
ρ=3.0×10−3×2.827×10−51.0=8.481×10−8Ω⋅m
The area Ad of the disc can also be calculated using the formula for the area of a circle:
Ad=πr2d
where rd is the radius of the disc. The diameter of the disc is given as 2.0cm, so the radius rd is:
rd=2.0cm2=1.0cm=1.0×10−2m
Now, substituting the radius into the area formula:
Ad=π(0.01)2=π×1×10−4m2=3.142×10−4m2
Now we can calculate the resistance Rd of the disc using the formula:
Rd=ρLdAd
where Ld is the thickness of the disc, which is 1.0mm=1.0×10−3m.
Rd=8.481×10−8×1.0×10−33.142×10−4
Calculating Rd:
Rd=8.481×10−113.142×10−4≈2.70×10−7Ω
The resistance between the round faces of the disc is approximately 2.7×10−7Ω.
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 DAILY TUTORIAL SHEET-2
Explore 15 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 DAILY TUTORIAL SHEET-3
Explore 15 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-0 LONG ANSWER TYPE
Explore 3 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
A 1m long wire of diameter 0.31mm has a resistance of 4.2Ω. If it is replaced by another wire of same material of length 1.5m and diameter 0.155mm, then the resistance of wire is
View SolutionDimensions of a block are 1cm×1cm×100cm. If specific resistance of its material is 3×10−7ohm−m, then the resistance between the opposite square faces is
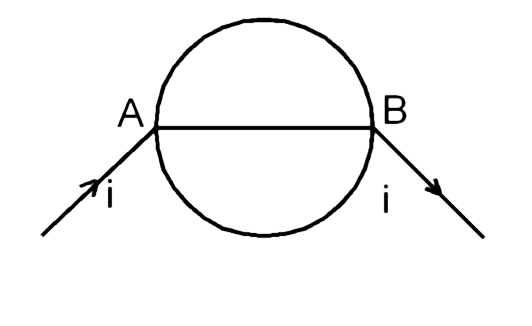
View SolutionA wire of resistance 0.5ohmm−1 is bent into a circle of radius 1m. The same wire is connected across a diameter AB as shown in fig. The equivalent resistance is
View SolutionA rod of length 20 cm made of metal A expands by 0.075 when its temperature is raised from 0∘C to 100∘C. Another rod of a different metal B having the same length expands by 0.045 cm for the same change in temperature. A third rod of the same length is composed of two parts, one of metal A and other of metal B. This rod expands by 0.065 cm for the same change in temperature. The portion made of metal A has the length :
View SolutionDimensions of a block are 1cm×1cm×100cm. If specific resistance of its material is 3×10−7ohm−m, then the resistance between the opposite rectangular facesis
View Solution(a) Calculate the self-inductance of a solenoid that is tightly wound with wire of diameter 0.10cm, has a cross-sectional area 0.90cm2 and is 40cm long
(b) If the current through the solenoid decreases uniformly from 10 A to 0A in 0.10s, what is the emf induced between the ends of the solenoid?
View SolutionA metal rod (A) of 25cm length expands by 0.050cm when its temperature is raised from 0∘C to 100∘C. Another rod (B) of a different metal of length 40cm expamds by 0.040cm for the same rise in temperature. A third rod ( C) of 50cm length is made up of pieces of rods (A) and (B) placed end to end expands by 0.03cm on heating from 0∘C. Find the lengths of each portion of the composite rod.
View SolutionFind the mass of a 3.5 m long lead pipe, if the external diameter of the pipe is 2.4 cm, thickness of the metal is 2 mm and the mass of 1 cm3 of lead is 11.4 grams.
View SolutionFind the number of coins, 1.5 cm in diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
View SolutionFind the number of coins, 1.5 cm in diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
View Solution