A metallic ring of mass m and radius l (ring being horizontal) is falling under gravity in a region having a magnetic field. If z is the vertical direction, the z-component of magnetic field is BZ=BO(I+λz). If R is the resistance of the ring and if the ring falls with a velocity v, find the energy lost in the resistance. If the ring has reached a constant velocity, use the conservation of energy to determine v in terms of m, B, λ and acceleration due to gravity g.Solution in Gujrati
Magnetic flux linked with ring,
ϕ=ABcosθ(∵θ=0)
θ=Bzπl2
ϕ=B0(1+λz)πl2
Now according to Faraday.s law induced emf,
ε=dϕdt=ddt[B0(1+λz)πl2]
ε=B0πl2λdzdt
ε=B0πl2λv
Induced current I=SR
I=B0πl2λvR
Heat produced per unit time,
H=I2R=(Bπl2λvR)2R
H=B20π2l4λ2v2R
This heat per unit time is produced at the cost of rate of change of potential energy.
Rate of change of P.E. = Heat produced per unit time
(∵ Here that K.E. remains constant)
ddt(mgz)=H
mg(dz)dt=B20π2l4λ2v2R
∴mgv=B20π2l4λ2v2R
∴v=mgRB20π2l4λ2
which is required equation of terminal velocity .
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (From DARPAN Based on Textbook )
121 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )
38 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section C Ncert Exemplar Solution (Short Answer )
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
14 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
Similar Questions
When a metallic rod falls freely, keeping its length horizontal and parallel to north-south direction, emf induced across it is ______
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionA magnetic field in a certain region is given by →B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=π2ω,πω and t=3π2ω.
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionA vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,

View SolutionA metallic ring of field. If z is the radius l (ring being horizontal is falling under gravity in a region haivng a magnetic field. If z is the vertical direction, the z-component of magnetic field is B_(z) = B_(0) (1 + lambda z) . If R the resistance of the ring and if the ring falls with a velocity upsilon , find the energy lost in the resistance If the ring has reached a constant velocity, use the conservation of energy to determine upsilon in terms of m, B, lambda and acceleration due to gravity g.
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
View SolutionA metallic ring with a small cut is held horizontally and a magnet is allowed to fall vertically through the ring then the acceleration of the magnet is :
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA metallic ring with a small cut is held horizontally and a magnet is allowed to fall vertically through the ring then the acceleration of the magnet is :
View Solutionएक अर्द्धवृत्ताकार वलय जिसकी त्रिज्या R है अपने तल के लम्बवत क्षैतिज चुम्बकीय क्षेत्र B में गिर रही है। MNQ स्थिति पर वलय की चाल है तथा वलय में विभवान्तर है
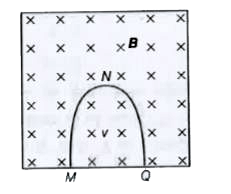
View SolutionA thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is
View Solutionत्रिज्या R की एक पतली अर्द्धवृत्ताकार धात्विक वलय क्षैतिज चुम्बकीय प्रेरण B में इस प्रकार गिर रही है कि इसका तल ऊर्ध्वाधर रहता है। जब यह वलय MNQ की स्थिति में पहुँचती है तब इसका वेग । है। इस समय अर्द्धवृत्ताकार वलय में उत्पन्न विभवान्तर होगा

View SolutionA metallic ring of field. If z is the radius l (ring being horizontal is falling under gravity in a region haivng a magnetic field. If z is the vertical direction, the z-component of magnetic field is Bz=B0(1+λz). If R the resistance of the ring and if the ring falls with a velocity υ, find the energy lost in the resistance If the ring has reached a constant velocity, use the conservation of energy to determine υ in terms of m, B, λ and acceleration due to gravity g.
View Solution
