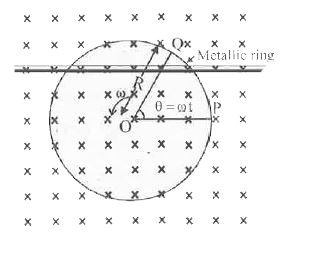
A metallic rod of 1m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular me tallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring (see figure). A constant and uniform magnetic field of 1T parallel to the axis present everywhere. What is the emf between the centre and the metallic ring?
 Solution in Tamil
Solution in Tamil
Method I
As stated in this question 6, during rotation, electrons are shifted to the end Q, creating an emf. Under steady state, emf acrosss a length dr is dɛ=Bvdr. Using equation ɛ=Blv, the magnitude of the emf generated across a length dr of the rod as it moves at right angles to the magnetic field is given by
∴ɛ=∫dɛ=R∫0Bvdr=R∫0Bωrdr=BωR22
But v=ωr. This gives ε=12×1.0×2π×50×(12)=157V
Method II
Considering the positions OP and OQ, the emf produced depends on rate of change of flux which itself is proportional to rate of sweeping of area of the sector. If θ is the angle between the rod and the radius of the circle at P at time t, the area of the sector OPQ is given by πR2×θ2π=12R2θ, where R is the radius of the circle. Hence, the induced emf is ε=B×ddt[12R2θ]=12BR2dθdt=BωR22
[Note: dθ2=ω=2πv]
The same expression we got earlier.
Topper's Solved these Questions
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - SOLUTIONS TO EXERCISES FROM NCERT TEXT14videos
ELECTROMAGNETIC INDUCTION
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - PRACTICE PROBLEMS FOR SELF ASSESSMENT3videos
ELECTROMAGNETIC INDUCTION
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Competitive Exam Corner20videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - COMPETITIVE EXAM CORNER16videos
ELECTROMAGNETIC WAVES
Similar Questions
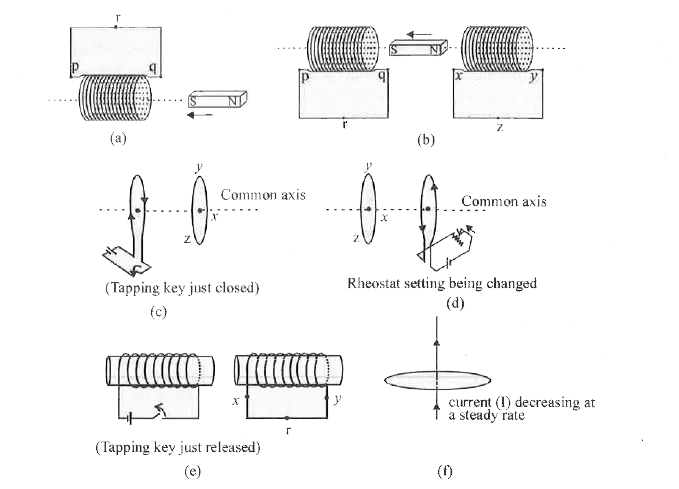
Predict the direction of induced current in the situations described by the following figures (a) to (f).
 06:37View Solution
06:37View SolutionA long solenoid with 15 turns per cm has a small loop area 2.0cm2 placed inside the solenoid normal to its axis. If the current carried by the solenoid changed steadiy from 2.0A to 4.0A in 0.1 s, what is the induced emf in the loop while the current is changing?
View SolutionTwo charged spherical conductors of radii R1andR2 are connected by a wire. Then the ratio of surface charge densitites of the spheres σ1/σ2 is
06:37View SolutionIf the total electromagnetic energy falling on a surface is U, then the total momentum delivered (for complete absorption) is
04:37View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
05:42View SolutionA metallic rod of length 'I' is rotated with a frequency with one end hinged at the center and the other end at the circumference of a circular metallic ring of radius r , about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present everywhere . Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtained the expression for it.
04:25View Solution1 मीटर लंबी धातु की एक छड़ को 50 चक्कर/सेकंड की आवृति से घुमाया गया है | छड़ के एक सिरा वृताकार धात्विक वलय जिसकी त्रिज्या 1 मीटर है, के केंद्र पर तथा दूसरा सिरा वलय की परिधि पर कब्जे से इस प्रकार जुड़ा है कि छड़ की गति वलय के केंद्र से जाने वाले तथा वलय के ताल में अभिलंबावत अक्ष के पारित: है (चित्र 6.11) | अक्ष के अनुदिश एक स्थिर तथा एकसमान चुंबकीय क्षेत्र 1 T सर्वत्र उपस्थित है | केंद्र तथा धात्विक वलय के बिच विधुत वाहक बल क्या होगा ?
 03:05View Solution
03:05View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
03:06View SolutionA metallie rod of 1 m length is rotated with a frequency of 50 revis, with one end hinged at the centre and the other end at the eireumference of a circular metallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring as in figure. A constant and uniform magnetic field of the parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?
 06:14View Solution
06:14View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring (Fig.). A constant and uniform magnetic field of 1 T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?
04:33View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
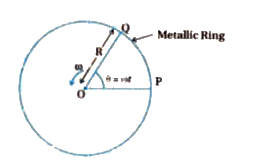
02:07View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring as per figure. A constant and uniform magnetic field of 1T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring ?
 View Solution
View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of length 'I' is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circualr metallic ring of a radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View Solution

