A metallic rod of length .L. is rotated with angular frequency of .ω. with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius R, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
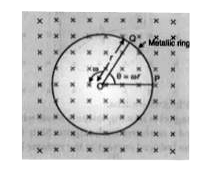
The magnitude of the emf, generated across a length dr of the rod, as it moves at right angles to the magnetic field, is given by
dε=Bvdr.
Therefore,
ε=∮dε=∫R0Bvdr=∫R0∫Bωrdr=BωR22
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION BOOK - OSWAAL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - TOPIC-1 (Faraday.s Laws & Lenz.s Law) ( Short Answer Type Questions-II)
4 Videos
- ELECTROMAGNETIC INDUCTION BOOK - OSWAAL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - TOPIC-1 (Faraday.s Laws & Lenz.s Law) (Long Answer Type Questions)
3 Videos
- ELECTROMAGNETIC INDUCTION BOOK - OSWAAL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - TOPIC-2 (Eddy Current, Self & Mutual Inductance) (Numerical Problems)
3 Videos
- ELECTRIC CHARGES & FIELDSBOOK - OSWAAL PUBLICATIONCHAPTER - ELECTRIC CHARGES & FIELDSEXERCISE - (TOPIC -2)Numerical Problems
5 Videos
- ELECTROMAGNETIC WAVESBOOK - OSWAAL PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - TOPIC-2 : ELECTROMAGNETIC SPECTRUM (SHORT ANSWER TYPE QUESTIONS)
7 Videos
Similar Questions
A metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View Solution
Knowledge Check
A metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
A157VB117VC127VD137V
A metallic rod of length 'I' is rotated with angular frequency of 'ω' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 'l', about an axis passing through its centre and perpendicular to the plane of ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of length 'l' is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
View SolutionA metallic rod of length 'I' is rotated with a frequency with one end hinged at the center and the other end at the circumference of a circular metallic ring of radius r , about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present everywhere . Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtained the expression for it.
View SolutionA metallic rod of length 'I' is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circualr metallic ring of a radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View Solution
