
A metre stick swinging in vertical plane about a fixed horizontal axis passing through its one end undergoes small oscillation of frequency f0. If the bottom half of the stick were but off, then its new frequency of small oscillation woul become.
f0
√2f0
2f0
2√2f0
The correct Answer is:B
f0=12π√mglI
where l is the distance between point of suspension and centre of mass of the body. Thus, for the stick of length L and mass m,
f0=12π
⎷mg(L)4m2(L2)212=12π√12gL=√2f0
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions

A metre stick swinging in vertical plane about a fixed horizontal axis passing through its one end undergoes small oscillation of frequency f0. If the bottom half of the stick were cut off, then its new frequency of small oscillation will become.
View SolutionA metre stick swinging about its one end oscillates with frequency f0. If the bottom half of the stick was cut off, then its new oscillation frequency will be :
View SolutionA magnetic needle vibrates in a vertical plane parallel to the magnetic meridlian about a horizontal axis passing through its centre. Its frequency is π. If the plane of oscillation is turned about a vertical axis by 90∘, the frequency of oscillation in vertical plane will be :
View SolutionA massless stick of length L is hinged at one end and a mass m attached to its other end. The stick is free to rotate in vertical plane about a fixed horizontal axis passing through frictionless hinge. The stick is held in a horizontal position. At what distance x from the hinge should a second mass M = m be attached to the stick, so that stick falls as fast as possible when released from rest

View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionAn almost inertia-less rod of length l3.5 m can rotate freely around a horizontal axis passing through its top end. At the bottom end of the roa a small ball of mass m andat the mid-point another small ball of mass 3m is attached. Find the angular frequency (in SI units) of small oscillations of the system about the equilibrium position. Gravitational acceleration is g=9.8 m//s^(2).

View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View SolutionAn uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upwards, then about the fixed axis.
STATEMENT-1 : Angular speed of the disc about the aixs of rotation will increase.
and
STATEMENT-2 : Moment of inertia of the disc is decreased about the axis of rotation.
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

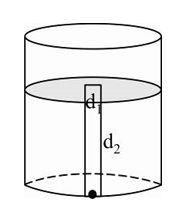
View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
View Solution
