A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time

A

at the highest position of the platform

B

at the mean position of the platform

C

for an amplitude of gω2

D

for and amplitude of √gω

Text Solution
Verified by Experts

The correct Answer is:A, C

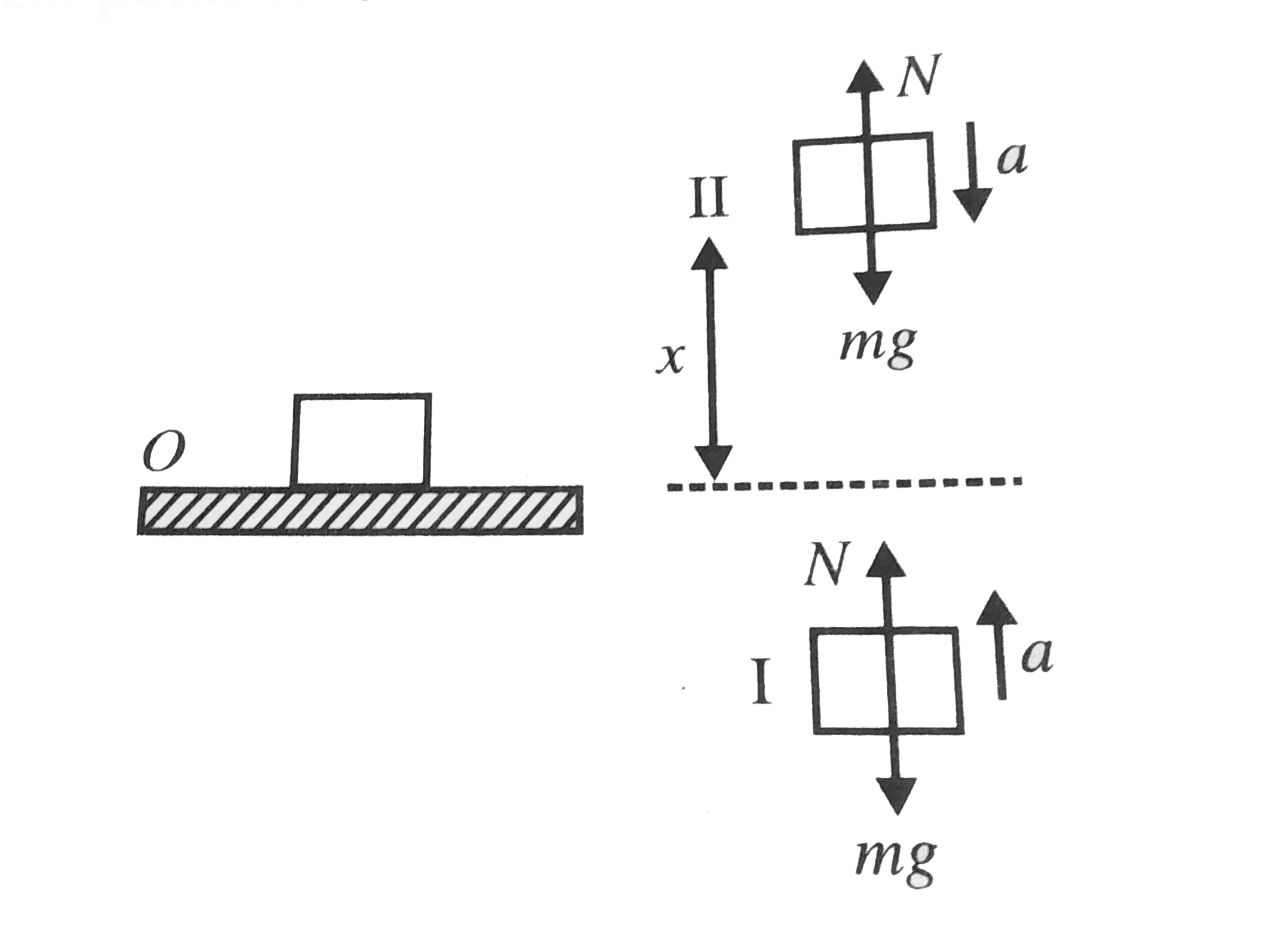
ocr_image
Let O be the mean position and a be the acceleration at a displacement x from O
At position I, N−mg=ma
N≠0
At position II, mg−N=ma
For N=0 (lost of contant), g=a=ω2x.
Loss of contact will occur for amplitude xmax=gω2 at the highest point of the motion.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11PHYSICSSIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In the previous question, the angular frequency of the simple harmonic motion is ω. The coefficient of friction between the coin and the platform is μ. The amplitude of oscillation is gradually increased. The coin will begin to slip on the platform for the first time
    (i) at the extreme positions of oscillations
    (ii) at the mean position
    (iii) for an amplitude of μgω2
    (iv) for an amplitude of gμω2

    A(i),(iii)
    B(ii), (iii)
    C(i), (iv)
    D(ii),(iv)

  • A coin is placed on a horizontal platform, which undergoes horizontal simple harmonic motion about a mean position O. The coin does not slip on the platform. The force of friction acting on the coin is F.
    (i) F is always directed towards O
    (ii) F is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
    (iii) F=0 when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
    (iv) F is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motion

    AF is always directed towards O
    BF is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
    CF=0 when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
    DF is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motion

  • A block of 0.5kg is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of 0.5Hz. The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly

    A0.5m
    B0.75m
    C1m
    D1.2m