A monkey a mass 15 kg is climbing on a rope with one end fixed to the ceiling. If it whishes to go up with an acceleration of , how much force should it apply to the rope? If the rope is 5 m long and the monkey starts from rest, how much time will it take to reach the ceiling?
To solve the problem step by step, we will break it down into two parts: calculating the force the monkey needs to apply to the rope and determining the time it takes for the monkey to reach the ceiling.
Part 1: Calculating the Force Applied by the Monkey
1. Identify the Given Data:
- Mass of the monkey, m=15kg
- Acceleration desired, a=1m/s2
- Gravitational acceleration, g=9.8m/s2 (we can approximate this to 10m/s2 for simplicity)
2. Calculate the Weight of the Monkey:
Weight(W)=m⋅g=15kg⋅10m/s2=150N
3. Apply Newton's Second Law:
According to Newton's second law, the net force acting on the monkey can be expressed as:
F−W=m⋅a
where F is the force applied by the monkey on the rope.
4. Substituting the Values:
F−150N=15kg⋅1m/s2
F−150N=15N
5. Solve for F:
F=150N+15N=165N
Part 2: Calculating the Time to Reach the Ceiling
1. Identify the Distance:
- Length of the rope (distance to the ceiling), s=5m
2. Use the Second Equation of Motion:
The second equation of motion states:
s=ut+12at2
where u is the initial velocity (which is 0 since the monkey starts from rest).
3. Substituting the Values:
5m=0⋅t+12⋅1m/s2⋅t2
Simplifying gives:
5=12t2
4. Solve for t2:
t2=5⋅2=10
5. Calculate t:
t=√10≈3.16s
Final Answers:
- The force the monkey should apply to the rope is 165 N.
- The time taken to reach the ceiling is approximately 3.16 seconds.
- Mass of the monkey, m=15kg
- Acceleration desired, a=1m/s2
- Gravitational acceleration, g=9.8m/s2 (we can approximate this to 10m/s2 for simplicity)
2. Calculate the Weight of the Monkey:
Weight(W)=m⋅g=15kg⋅10m/s2=150N
According to Newton's second law, the net force acting on the monkey can be expressed as:
F−W=m⋅a
where F is the force applied by the monkey on the rope.
F−150N=15kg⋅1m/s2
F−150N=15N
F=150N+15N=165N
- Length of the rope (distance to the ceiling), s=5m
The second equation of motion states:
s=ut+12at2
where u is the initial velocity (which is 0 since the monkey starts from rest).
5m=0⋅t+12⋅1m/s2⋅t2
Simplifying gives:
5=12t2
t2=5⋅2=10
t=√10≈3.16s
- The force the monkey should apply to the rope is 165 N.
- The time taken to reach the ceiling is approximately 3.16 seconds.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
9 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
A can of paint with a mass of 6 kg hangs from a rope. If the can is to be pulled up to a rooftop with an acceleration of 1m/s, what must be the tension in the rope ?
View SolutionA can of paint with a mass of 6 kg hangs from a rope. If the can is to be pulled up to a rooftop with an acceleration of 1m/s2, what must be the tension in the rope ?
View SolutionHow much force is required to cause an object of mass 2 kg to have an acceleration of 4m/s2 ?
View SolutionTwo blocks of mass 10kg and 2kg respectively are connected by an ideal string passing over a fixed smooth pulley as shown in figure. A monkey of mass 8kg started climbing the string with a constant acceleration of 2m/s2 with respect to string at t=0 . Initially the system is in equilibrium and monkey is at a distance 2.4 from the pulley. Find the time taken by monkey to reach the pulley in sec.
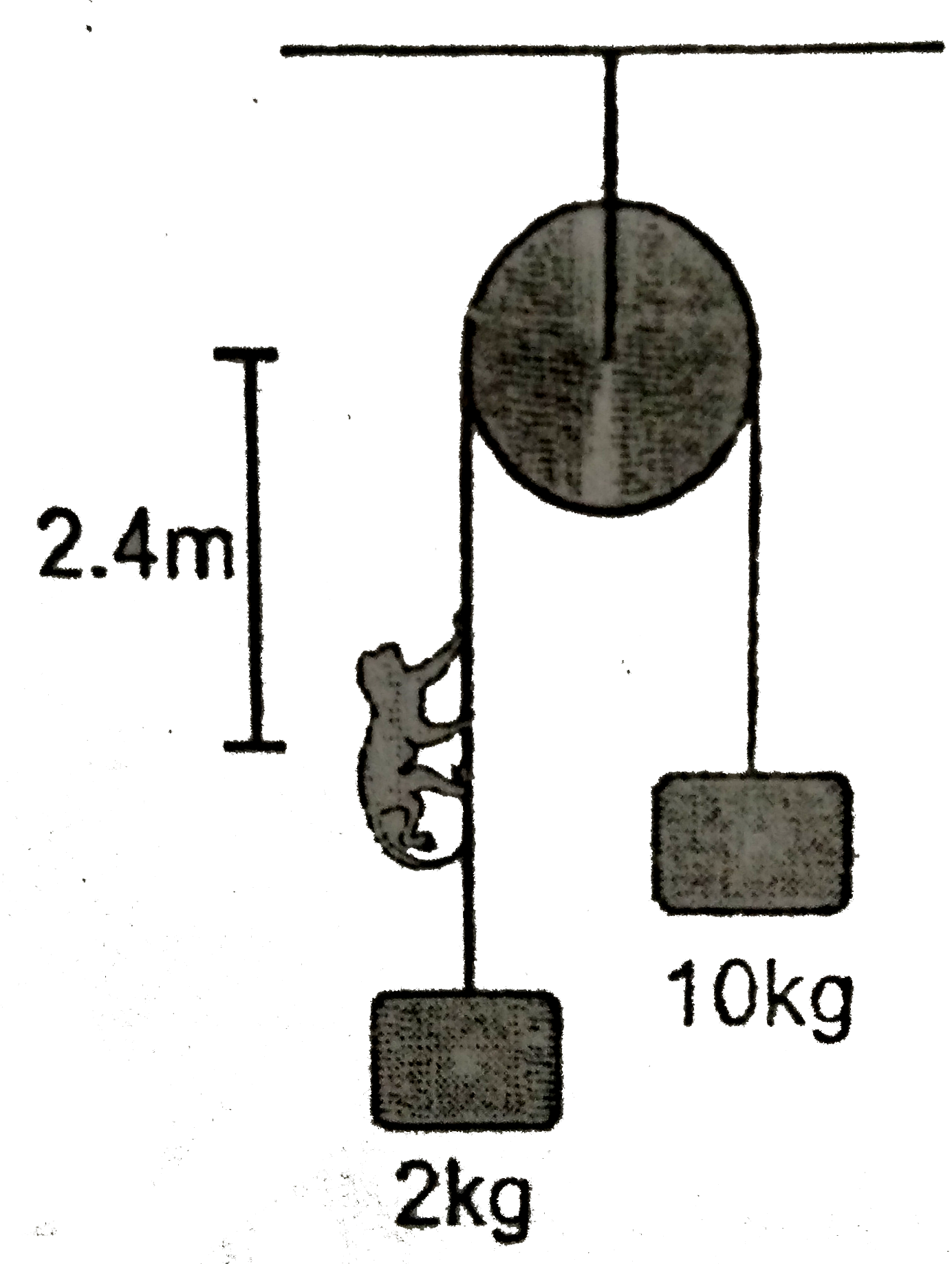
View SolutionA uniform rope of mass m hangs freely from a ceiling. A bird of mass M climbs up the rope with an acceleration a. The force exerted by the rope on the ceiling is
View SolutionA monkey A (mass = 5kg) is climbing up a rope tied to a rigid support. The monkey B (mass = 2kg) is holding on to the tail of monkey A. If the tail can tolerate a maximum tension of 30N, what force should monkey A apply on the rope in order to carry monkey B with it? (g=10m/s2).
View SolutionA money of mass 40 kg climbs up a rope, of breaking load 600 N hanging from a ceiling. If it climbs up the rope with the maximum possible acceleration, then the time taken by monkey to climb up is [length of rope is 10 m]
View SolutionSee Fig 5.8 .A mass of 6 kg is suspended by a rope of length 2m from the ceiling . A force of 50 N in the horizontal direction is applied at the mid-point P of the rope, as shown. What is the angle the rope makes with the vertical in equilibrium ? (Take g = 10 m s−2). Neglect the mass of the rope.
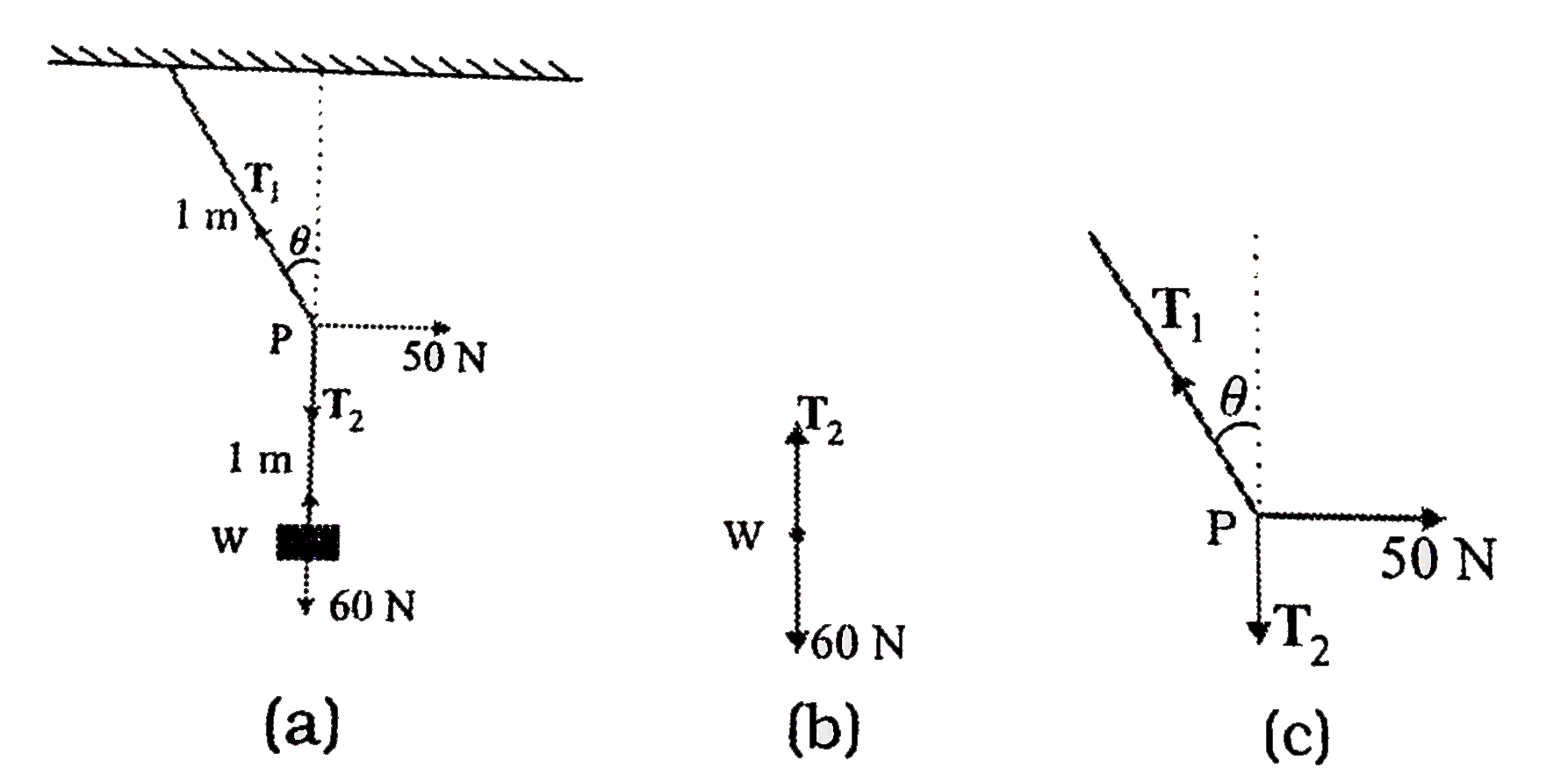
View SolutionTwo monkey of masses 10 kg and 8 kg are moving along a verticle rope as shown in fig. the former climbing up with an acceleration of 2ms−2, while the later coming down with a uniform velocity of 2ms−2. Find the tension in the rope at the fixed support.

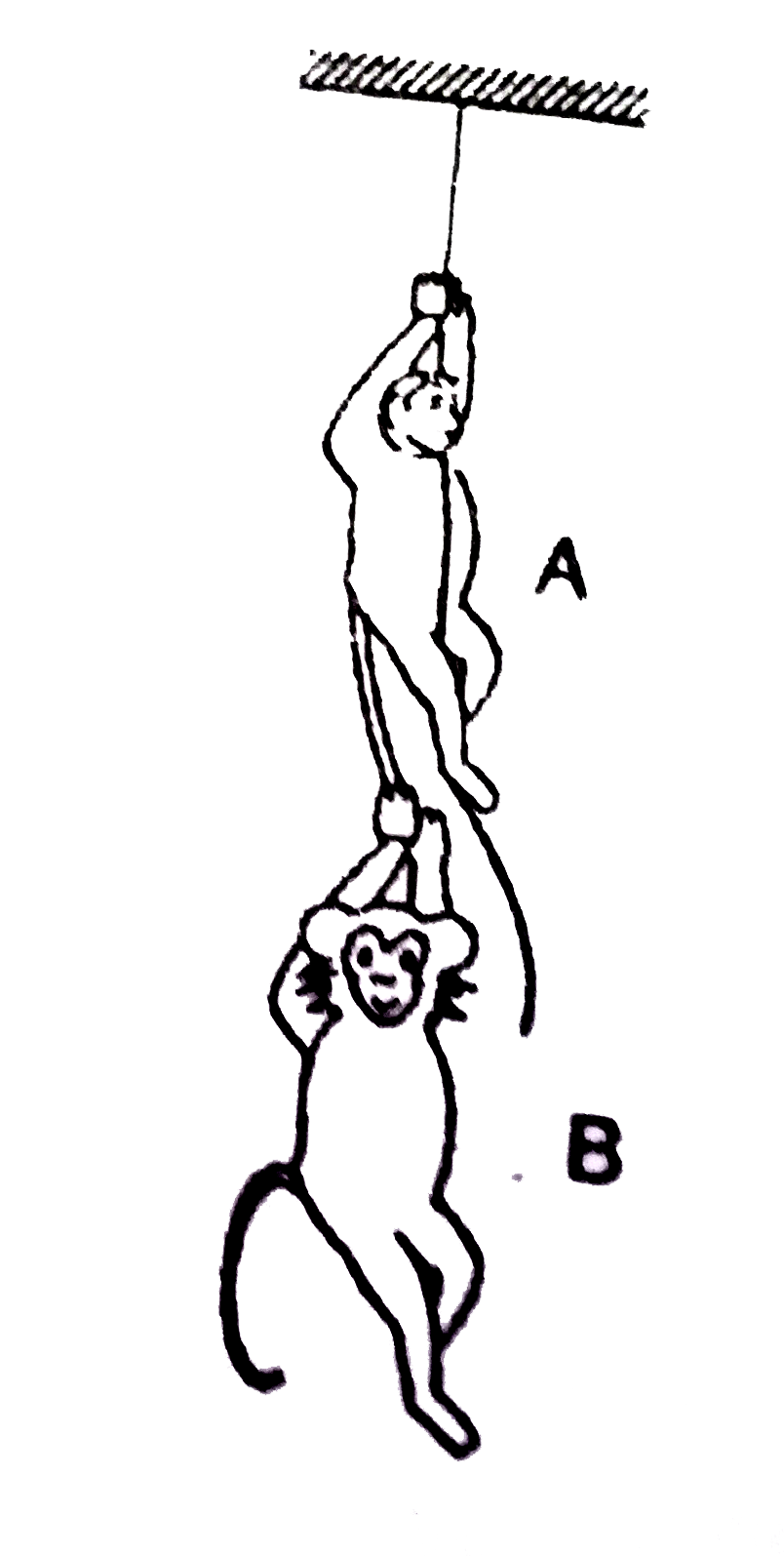
View SolutionThe monkey B shown in fig. is holding on to the tall of the monkey A which is climbing up a rope. The masses of the monkeys A and B are 5 kg and 2kg respectively. If A can tolerate a tension of 30N in its tall, what force should it apply on the rope in order to carry the monkey B with it ?
(Take g=10ms−2)
View Solution
