A monkey of mass m moving up on a massless string so as to just lift a block of mass M. After some time the monkey stops moving w.r.t the string. Find the magnitude of the change in the monkey's acceleration.
To solve the problem step by step, we will analyze the forces acting on both the monkey and the block, and derive the equations for their accelerations.
Step 1: Understand the system
We have a monkey of mass m climbing up a massless string, which is lifting a block of mass M. Initially, the monkey is moving upwards with some acceleration a1.
Step 2: Draw Free Body Diagrams
1. For the Monkey:
- The forces acting on the monkey are:
- Weight mg acting downwards.
- Tension T acting upwards.
- The equation of motion for the monkey can be written as:
T−mg=ma1(1)
Rearranging gives:
T=ma1+mg(2)
2. For the Block:
- The forces acting on the block are:
- Weight Mg acting downwards.
- Tension T acting upwards.
- The block is at rest while the monkey is climbing, so:
T−Mg=0(3)
Rearranging gives:
T=Mg(4)
Step 3: Equate Tension from Both Equations
From equations (2) and (4), we can set the expressions for tension equal to each other:
ma1+mg=Mg
Rearranging gives:
ma1=Mg−mg
Thus, we can express the monkey's acceleration a1:
a1=Mg−mgm=g(M−mm)(5)
Step 4: Analyze the System When the Monkey Stops Moving
When the monkey stops moving with respect to the string, the entire system (monkey + block) will have a new acceleration a2. The forces acting on the system can be analyzed similarly.
1. For the combined system (Monkey + Block):
- The total mass is m+M.
- The tension will now be:
T=mg+ma2(6)
And for the block:
Mg−T=(M+m)a2(7)
Rearranging gives:
T=Mg−(M+m)a2(8)
Step 5: Equate Tension Again
Setting equations (6) and (8) equal:
mg+ma2=Mg−(M+m)a2
Rearranging gives:
mg+ma2+(M+m)a2=Mg
mg+(m+M)a2=Mg
Thus, we can express a2:
(m+M)a2=Mg−mg
a2=Mg−mgm+M=g(M−mm+M)(9)
Step 6: Find the Change in Acceleration
Now, we need to find the change in acceleration Δa:
Δa=a2−a1
Substituting equations (5) and (9):
Δa=g(M−mm+M)−g(M−mm)
Factoring out g(M−m):
Δa=g(M−m)(1m+M−1m)
Finding a common denominator:
Δa=g(M−m)(m−(M+m)m(m+M))
Simplifying gives:
Δa=g(M−m)(m−M)m(m+M)=−g(M−m)2m(m+M)
Final Result
The magnitude of the change in the monkey's acceleration is:
Δa=g(M−m)2m(m+M)
We have a monkey of mass m climbing up a massless string, which is lifting a block of mass M. Initially, the monkey is moving upwards with some acceleration a1.
1. For the Monkey:
- The forces acting on the monkey are:
- Weight mg acting downwards.
- Tension T acting upwards.
- The equation of motion for the monkey can be written as:
T−mg=ma1(1)
Rearranging gives:
T=ma1+mg(2)
- The forces acting on the block are:
- Weight Mg acting downwards.
- Tension T acting upwards.
- The block is at rest while the monkey is climbing, so:
T−Mg=0(3)
Rearranging gives:
T=Mg(4)
From equations (2) and (4), we can set the expressions for tension equal to each other:
ma1+mg=Mg
Rearranging gives:
ma1=Mg−mg
Thus, we can express the monkey's acceleration a1:
a1=Mg−mgm=g(M−mm)(5)
When the monkey stops moving with respect to the string, the entire system (monkey + block) will have a new acceleration a2. The forces acting on the system can be analyzed similarly.
- The total mass is m+M.
- The tension will now be:
T=mg+ma2(6)
And for the block:
Mg−T=(M+m)a2(7)
Rearranging gives:
T=Mg−(M+m)a2(8)
Setting equations (6) and (8) equal:
mg+ma2=Mg−(M+m)a2
Rearranging gives:
mg+ma2+(M+m)a2=Mg
mg+(m+M)a2=Mg
Thus, we can express a2:
(m+M)a2=Mg−mg
a2=Mg−mgm+M=g(M−mm+M)(9)
Now, we need to find the change in acceleration Δa:
Δa=a2−a1
Substituting equations (5) and (9):
Δa=g(M−mm+M)−g(M−mm)
Factoring out g(M−m):
Δa=g(M−m)(1m+M−1m)
Finding a common denominator:
Δa=g(M−m)(m−(M+m)m(m+M))
Simplifying gives:
Δa=g(M−m)(m−M)m(m+M)=−g(M−m)2m(m+M)
The magnitude of the change in the monkey's acceleration is:
Δa=g(M−m)2m(m+M)
Similar Questions
The pulley shown in the diagram is frictionless. A cat of mass 1kg moves up on the massless string so as to just lift a block of mass 2kg. After some time, the cal stops moving with respect to the string. The magnitude of the change in the cat's accelration is
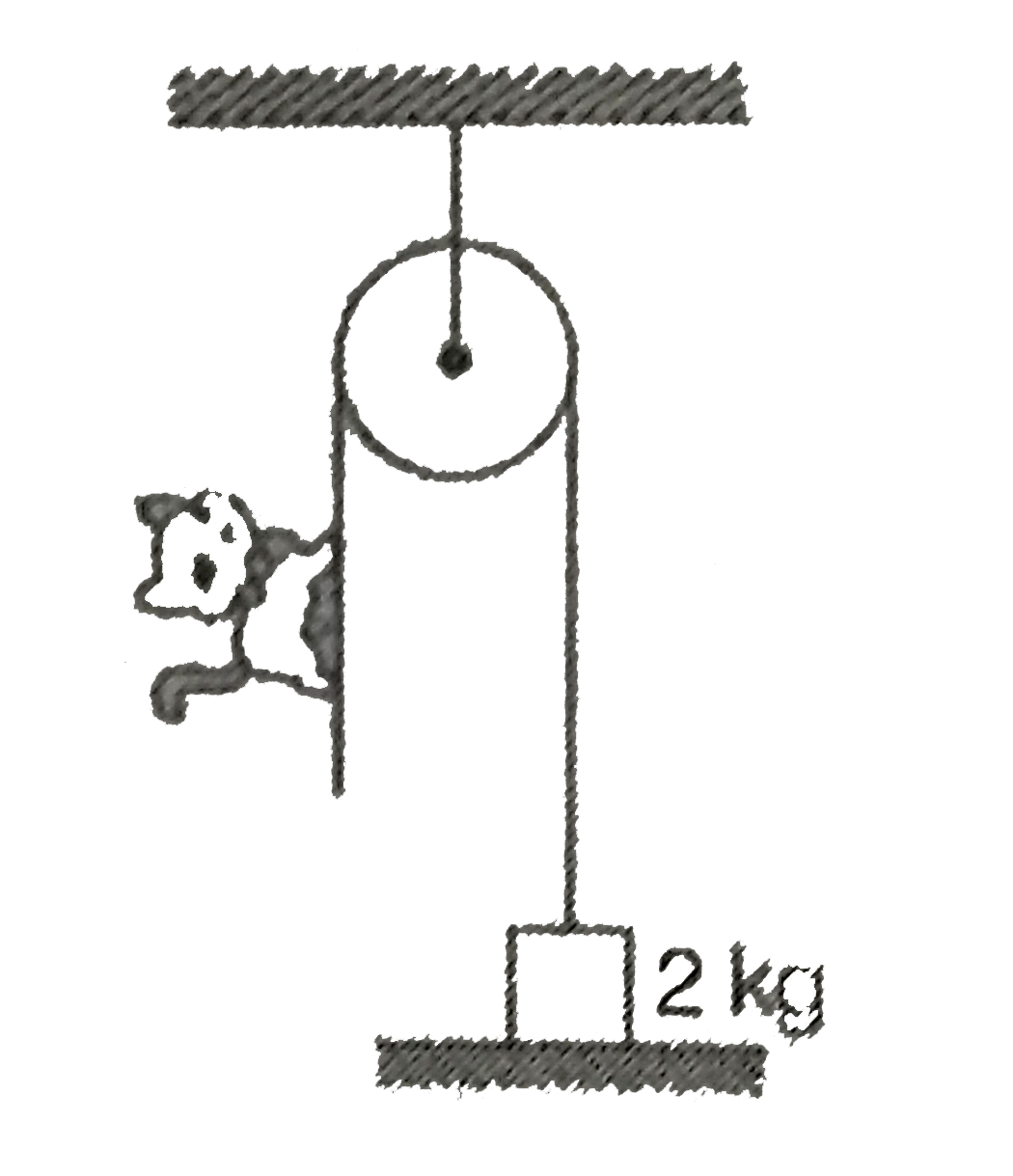
View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionTwo mankeys (a) and (b ) of same mass m=1 kg are hanging on the dtring such that block of amss 2 kg ramains at rest and it is given that monkeys( B) is just holding the string then which of the following statement (S) is /are correct (g=10m/s2)

View SolutionA block of mass m is attached with a massless in string. Breaking strength of string is 4mg. Block is moving up. The maximum acceleration and maximum retardation of the block can be

View SolutionA monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight .The monkey move downward with respect to the rope with an acceleration b.

The acceleration of weight is
View SolutionA monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The tension of rope is
View SolutionA block of mass m slides down on a wedge of mass M as shown in figure .Let a1 be the asseleration of the acceleration of and a2 the the acceleration od block 1N1 is the normal reaction between block and wedge and N2 the normal reaction between wedge and gound .frication is absent everwhere .Select the correct alternative(s)
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a function of the distance measured from the mass M (bottom of the string).

View Solution
