A uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
2MM+2mg
2mM+2mg
M+2m2Mg
2M+m2Mg
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the falling block and the torque acting on the disc. Let's break it down step by step.
Step 1: Identify the Forces Acting on the Block
The block of mass m is subject to two forces:
- The gravitational force acting downward: Fg=mg
- The tension T in the string acting upward.
According to Newton's second law, the net force acting on the block can be expressed as:
Fnet=mg−T=ma
where a is the acceleration of the block.
Step 2: Express Tension in Terms of Acceleration
From the equation derived in Step 1, we can rearrange it to find the tension T:
T=mg−ma
This is our equation (1).
Step 3: Analyze the Torque on the Disc
The tension in the string also creates a torque on the disc. The torque τ can be expressed as:
τ=T⋅R
where R is the radius of the disc.
Step 4: Relate Torque to Angular Acceleration
The torque is also related to the moment of inertia I and angular acceleration α of the disc:
τ=Iα
For a uniform disc, the moment of inertia I about its center is given by:
I=12MR2
Thus, we can write:
T⋅R=12MR2α
Since the linear acceleration a of the block is related to the angular acceleration α of the disc by the equation:
α=aR
we can substitute this into the torque equation:
T⋅R=12MR2⋅aR
This simplifies to:
T=12Ma
This is our equation (2).
Step 5: Substitute Tension into the Block's Equation
Now we have two expressions for tension:
1. From the block: T=mg−ma
2. From the disc: T=12Ma
Setting these equal gives:
mg−ma=12Ma
Step 6: Rearranging the Equation
Rearranging the above equation to solve for a:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Thus, we can solve for a:
a=mgm+12M
Final Step: Simplifying the Expression
To express a in a simpler form:
a=2mg2m+M
Conclusion
The magnitude of the acceleration of the falling block m is given by:
a=2mg2m+M
The block of mass m is subject to two forces:
- The gravitational force acting downward: Fg=mg
- The tension T in the string acting upward.
Fnet=mg−T=ma
where a is the acceleration of the block.
From the equation derived in Step 1, we can rearrange it to find the tension T:
T=mg−ma
This is our equation (1).
The tension in the string also creates a torque on the disc. The torque τ can be expressed as:
τ=T⋅R
where R is the radius of the disc.
The torque is also related to the moment of inertia I and angular acceleration α of the disc:
τ=Iα
For a uniform disc, the moment of inertia I about its center is given by:
I=12MR2
Thus, we can write:
T⋅R=12MR2α
Since the linear acceleration a of the block is related to the angular acceleration α of the disc by the equation:
α=aR
we can substitute this into the torque equation:
T⋅R=12MR2⋅aR
This simplifies to:
T=12Ma
This is our equation (2).
Now we have two expressions for tension:
1. From the block: T=mg−ma
2. From the disc: T=12Ma
mg−ma=12Ma
Rearranging the above equation to solve for a:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Thus, we can solve for a:
a=mgm+12M
To express a in a simpler form:
a=2mg2m+M
The magnitude of the acceleration of the falling block m is given by:
a=2mg2m+M
Similar Questions
A uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
View SolutionFig. shows a uniform disc of mass 1 kg and radius 0.2 m mounted on an axle supported in fixed frictionless bearings. A light string is wrapped around the rim of the wheel. A constant downwards pull of 2 kg wt. is exerted on the string. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ?
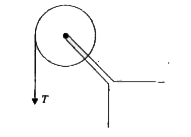
View SolutionA uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
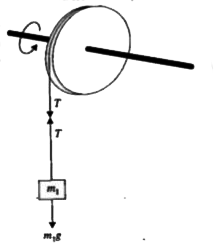
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
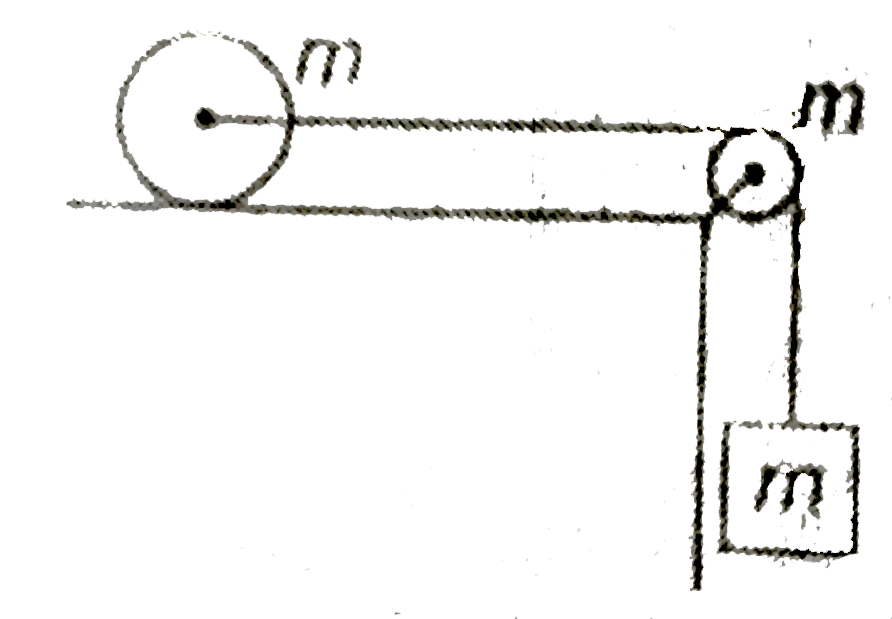
Acceleration of the block is
View SolutionA disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
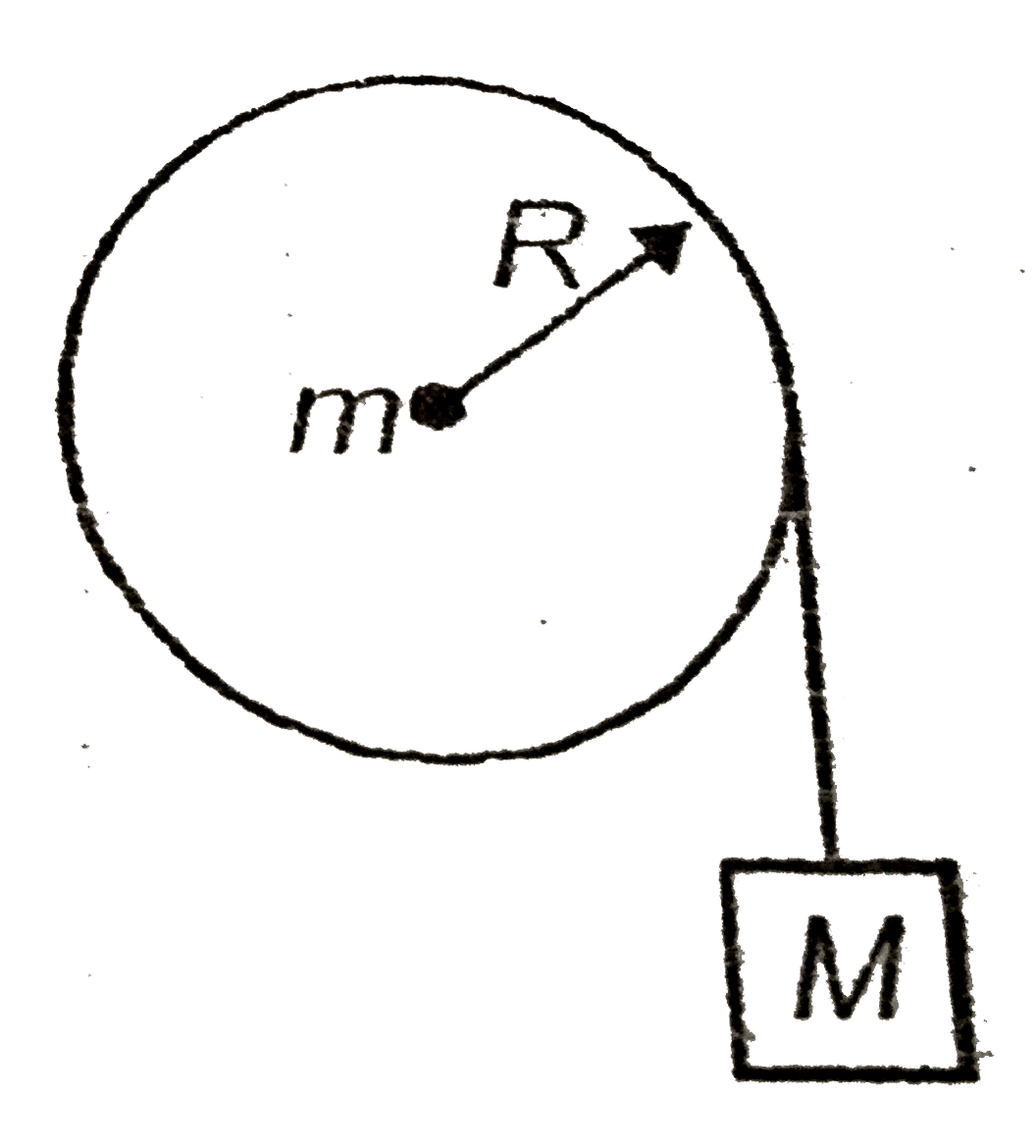
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
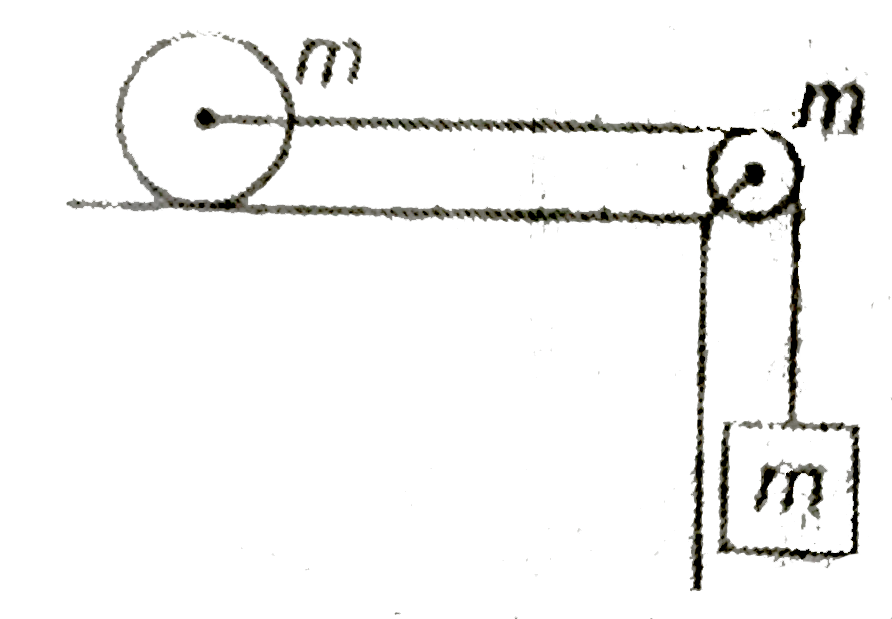
Angular acceleration of the cylinder is
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
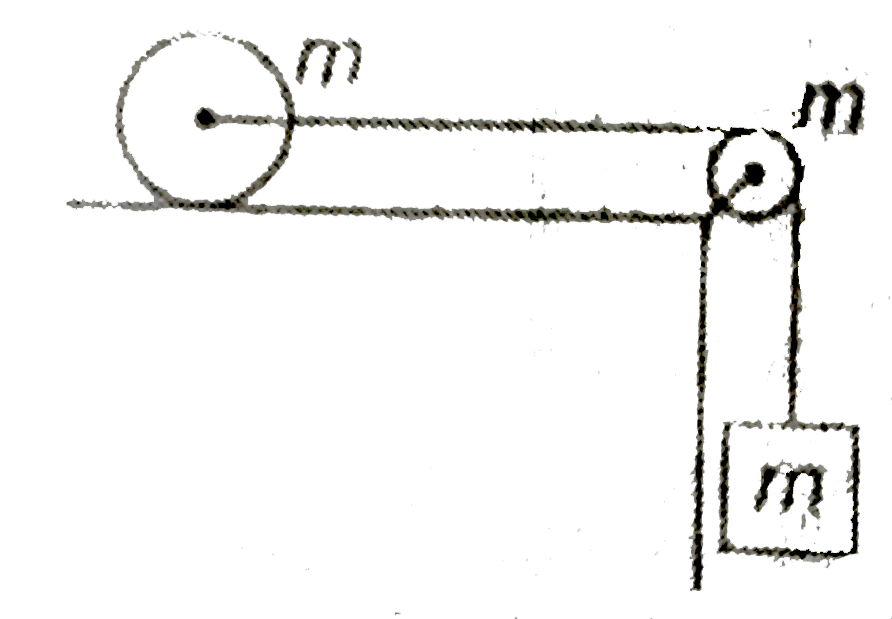
Force of friction acting on the cylinder is
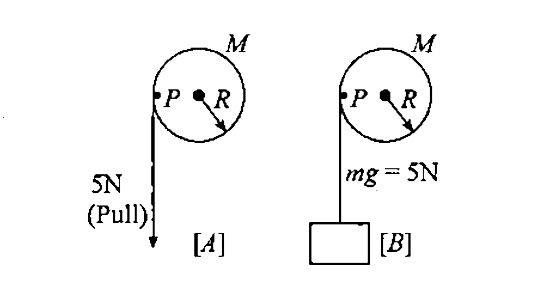
View SolutionA uniform disc of mass M =2.50 kg and radius R=0.20 m is mounted on an axle supported on fixed frictionless bearings. A light cord wrapped around the rim is pulled with a force 5 N. On the same system of pulley and string, instead of pulling it down, a body of weight 5 N is suspended. If the first processis termed A and the second B, the tangential acceleration of point P will be:
View Solution