A monochromatic light is travelling in a medium of refractive index n = 1.6. It enters a stack of glass layers from the bottom side at an angle θ=30∘. The interfaces of the glass layers are parallel to each other. The refractive indices of different glass layers are monotonically decreasing as nm=nmΔn, where nm is the refractive index of the mth slab and Δn = 0.1 (see the figure). The ray is refracted out parallel to the interface between the (m–1)th and mth slabs from the right side of the stack. What is the value of m ?

The correct Answer is:8
1.6sinθ=(n−mΔn)sin90∘
1.6sinθ=n−mΔn
1.6×12=1.6−m(0.1)
m×0.1=0.8
m = 8
Mathematically answer is 8, but this value of refractive index is physically impossible.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST14videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS)1videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
A monochromatic light is travelling in a medium of refractive index n = 1.6. It enters a stack of glass layers from the bottom side at an angle θ=30∘. The interfaces of the glass layers are parallel to each other. The refractive indices of different glass layers are monotonically decreasing as nm=n−mΔn, where nm is the refractive index of the mth slab and Δn=0.1 (see the figure). The ray is refracted out parallel to the interface between the (m–1)th and mth slabs from the right side of the stack. What is the value of m?
 View Solution
View SolutionA light ray travelling in a medium of refractive index μ1 is incident on a parallel faced glass slab making an angle of θ with the glass surface. The refractive index of the medium on the other side of the glass slab is μ3(>μ1). Find the angular deviation suffered by the light ray.
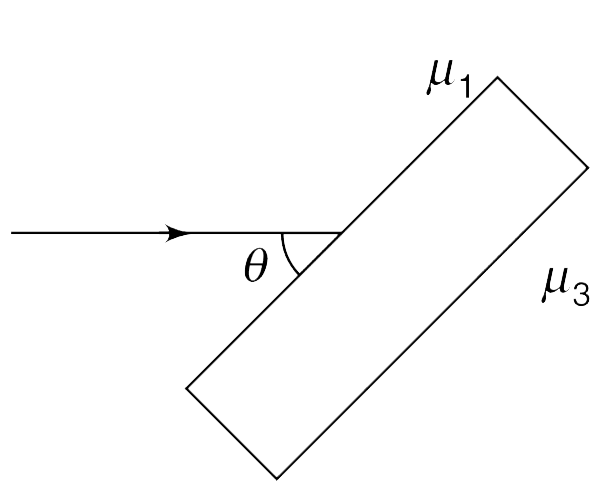 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Monochromatic light of wavelength λ1 travelling in medium of refractive index n1 enters a denser medium of refractive index n2. The wavelength in the second medium is
A(a) λ1(n1n2)B(b) λn2n1C(c) λ1D(d) λ(n2−n1n1) - Question 2 - Select One
A ray of light strikes a glass plate at an angle of 40∘. If the reflected and refracted rays are perpendicular to each other the index of refractive of glass is
A1/2B√3/2C3/2D0.83 - Question 3 - Select One
A monochromatic light of wavelength 4800 A travelling in air is incident on a glass slab of refractive index 1.5, its wavelenght in glass slab is
A5000 ÅB4800 ÅC3500 ÅD3200 Å
Refractive index of glass with respect to water is 1.125. What is the refractive index of water of refractive index of glass is 1.5.
View SolutionA ray of light travelling in glass (refractive index 1.52) enters water (refractive index 1.33) obliquely, The ray of light
View SolutionA ray of light is incident on a glass slab making an angle of 30∘ with the surface. The angle of refraction in glass, if the refractive index of flass is 1.6 , is
View SolutionA ray of light travels from a medium of refractive index n1 to
a medium of refractive index n2. If angle of incidence is i and
angle of refraction is r, than sinisinr is equal toView SolutionA ray of light is travelling from glass to air. (Refractive index of glass =1.5). The angle of incidence is 50∘. The deviation of the ray is
View Solution

