A mortar fires a shell of mass M which explodes into two pieces of mass M5 and 4M5 at the top of the trajectory. The smaller mass falls very close to the mortar. In the same time bigger piece lands a distance D from the mortar. The shell would have fallen at a distance R from the mortar if there was no explosion. The value of D is (neglect air resistance)
(a) 3R2
(b) 4R3
(c) 5R4
(d) None of these
The correct Answer is:C
To solve the problem step by step, we will analyze the situation involving the mortar, the shell, and the resulting pieces after the explosion.
Step 1: Understand the Problem
A mortar fires a shell of mass M that explodes into two pieces at the top of its trajectory. The masses of the pieces are M5 (smaller mass) and 4M5 (larger mass). The smaller mass falls very close to the mortar, while the larger mass lands a distance D from the mortar. We need to find the value of D in terms of R, the distance the shell would have fallen if there was no explosion.
Step 2: Analyze the Center of Mass
Since there is no external horizontal force acting on the system, the center of mass of the shell before and after the explosion will remain in the same horizontal position. Thus, the range covered by the center of mass before the explosion will equal the range covered by the center of mass after the explosion.
Step 3: Define the Center of Mass
The center of mass xCM for the two pieces after the explosion can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
where:
- m1=M5 (smaller mass)
- x1=0 (the smaller mass falls very close to the mortar)
- m2=4M5 (larger mass)
- x2=D (the distance where the larger mass lands)
Step 4: Set Up the Equation
Substituting the values into the center of mass equation:
xCM=(M5⋅0)+(4M5⋅D)M5+4M5=4M5DM=4D5
Step 5: Relate to the Original Range R
Before the explosion, the range R is simply the distance that the shell would have traveled. Since the center of mass does not change its horizontal position, we have:
R=xCM=4D5
Step 6: Solve for D
Now, we can rearrange the equation to solve for D:
D=5R4
Conclusion
Thus, the value of D in terms of R is:
D=5R4
A mortar fires a shell of mass M that explodes into two pieces at the top of its trajectory. The masses of the pieces are M5 (smaller mass) and 4M5 (larger mass). The smaller mass falls very close to the mortar, while the larger mass lands a distance D from the mortar. We need to find the value of D in terms of R, the distance the shell would have fallen if there was no explosion.
Since there is no external horizontal force acting on the system, the center of mass of the shell before and after the explosion will remain in the same horizontal position. Thus, the range covered by the center of mass before the explosion will equal the range covered by the center of mass after the explosion.
The center of mass xCM for the two pieces after the explosion can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
where:
- m1=M5 (smaller mass)
- x1=0 (the smaller mass falls very close to the mortar)
- m2=4M5 (larger mass)
- x2=D (the distance where the larger mass lands)
Substituting the values into the center of mass equation:
xCM=(M5⋅0)+(4M5⋅D)M5+4M5=4M5DM=4D5
Before the explosion, the range R is simply the distance that the shell would have traveled. Since the center of mass does not change its horizontal position, we have:
R=xCM=4D5
Now, we can rearrange the equation to solve for D:
D=5R4
Thus, the value of D in terms of R is:
D=5R4
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective32videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions1videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason15videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
A stationary shell of mass M explodes in to two parts and their masses are in the ratio 2:3, then the ratio of their deBroglie wavelengths is
View SolutionA bomb of mass 3.0kg explodes in air into two pieces of masses 2.0kg and 1.0kg. The smaller mass goes at a speed of 80m/s. The total energy imparted to the two fragments is :
View SolutionA bomb of mass 12 kg explodes into two pieces of masses 4 kg and 8 kg. The velocity of mass 4 kg is 20 m/s. Find the velocity of mass 8 kg.
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
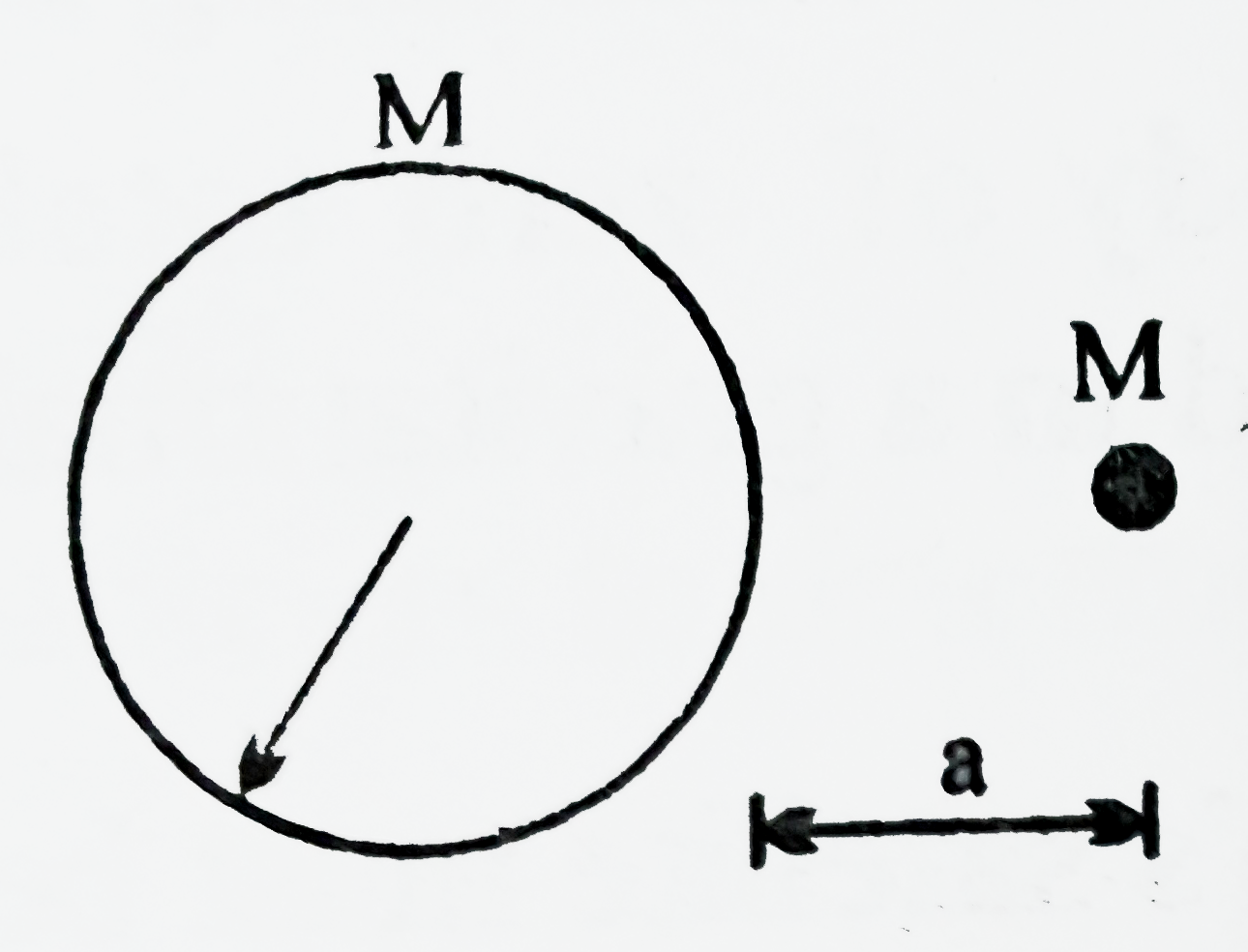 View Solution
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
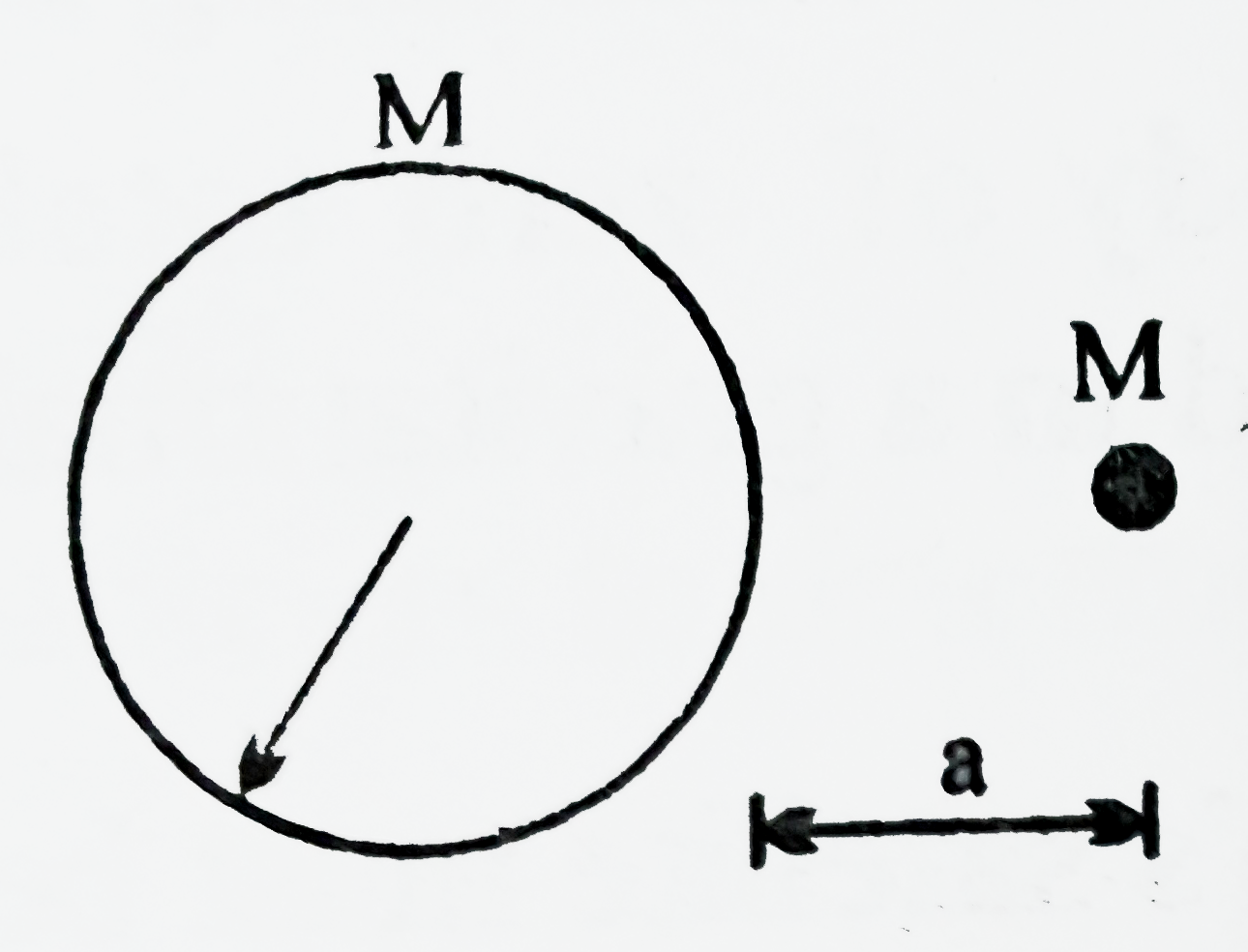 View Solution
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionA shell fired along a parabolic path explodes into two fragment of equal mass at the top of the trajectory. One of the fragment returns to the point of firing having retraced its original path. If v is the velocity of projectile at highest point, than
View SolutionA satellite A of mass m is at a distance of r from the centre of the earth. Another satellite B of mass 2m is at distance of 2r from the earth's centre. Their time periode are in the ratio of
View Solution

