In the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
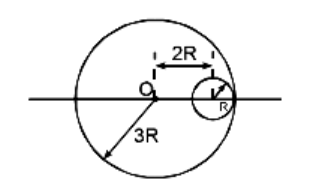
(a) R2
(b) R5
(c) R4
(d) None of these
The correct Answer is:C
xCM=A1x1−A2x2A1−A2
=π(3R)2(0)−(πR2)(2R)π(3R)2−πR2=−R4
∴ Distance of centre of mass from origin =R4
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective
32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the centre of mass of a uniform disc of radius a from which a circualr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionThe distance of the centre of mass of T-shaped uniform plate from O is :
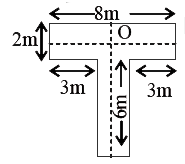
View SolutionFind the workdone to move an earth satellite of mass m from a circular orbit of radius 2R to one of radius 3R.
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionA uniform circular disc has a radius of 20cm. A circular disc of radius 10cm is cut concentrically from the original disc. The shift in centre of mass is
View Solution
