A moving block having mass m , collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the block is v, then the value of coefficient of restitution (e) will be
0.8
0.25
0.5
0.4
The correct Answer is:B
To solve the problem, we will use the principles of conservation of momentum and the definition of the coefficient of restitution.
1. Identify the masses and initial velocities:
- Mass of the moving block (m) = m
- Mass of the stationary block (4m) = 4m
- Initial velocity of the moving block (u1) = v
- Initial velocity of the stationary block (u2) = 0
2. Apply the conservation of linear momentum:
The total initial momentum before the collision must equal the total final momentum after the collision.
Initial momentum=Final momentum
mu1+4mu2=mv′1+4mv′2
Substituting the values:
mv+4m(0)=mv′+4m(v′2)
Simplifying:
mv=mv′+4mv′2
3. Determine the final velocities:
Since the lighter block (mass m) comes to rest after the collision, its final velocity v′1=0.
Substitute v′1=0 into the momentum equation:
mv=0+4mv′2
This simplifies to:
mv=4mv′2
Dividing both sides by m (assuming m≠0):
v=4v′2
Thus, we find:
v′2=v4
4. Calculate the coefficient of restitution (e):
The coefficient of restitution is defined as:
e=Relative velocity of separationRelative velocity of approach
- Relative velocity of separation: After the collision, the lighter block is at rest (0), and the heavier block moves with velocity v′2=v4. Thus, the relative velocity of separation is:
Relative velocity of separation=v′2−0=v4
- Relative velocity of approach: Before the collision, the relative velocity is:
Relative velocity of approach=v−0=v
5. Substituting values into the coefficient of restitution formula:
e=v4v=14
Final Answer:
The value of the coefficient of restitution e is 14.
- Mass of the moving block (m) = m
- Mass of the stationary block (4m) = 4m
- Initial velocity of the moving block (u1) = v
- Initial velocity of the stationary block (u2) = 0
The total initial momentum before the collision must equal the total final momentum after the collision.
Initial momentum=Final momentum
mu1+4mu2=mv′1+4mv′2
Substituting the values:
mv+4m(0)=mv′+4m(v′2)
Simplifying:
mv=mv′+4mv′2
Since the lighter block (mass m) comes to rest after the collision, its final velocity v′1=0.
Substitute v′1=0 into the momentum equation:
mv=0+4mv′2
This simplifies to:
mv=4mv′2
Dividing both sides by m (assuming m≠0):
v=4v′2
Thus, we find:
v′2=v4
The coefficient of restitution is defined as:
e=Relative velocity of separationRelative velocity of approach
- Relative velocity of separation: After the collision, the lighter block is at rest (0), and the heavier block moves with velocity v′2=v4. Thus, the relative velocity of separation is:
Relative velocity of separation=v′2−0=v4
- Relative velocity of approach: Before the collision, the relative velocity is:
Relative velocity of approach=v−0=v
e=v4v=14
The value of the coefficient of restitution e is 14.
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(JIPMER)
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
A block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View Solution
Knowledge Check
A body of mass m, moving with velocity μ collides elasticity with another body at rest having mass M. If the body of mass M moves with velocity V, then the velocity of the body of mass m after the impact is
Am−Mm+MμBm−Mm+MVCm+MVm+MDmu−MVm
A ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View SolutionA particle of mass m collides with another stationary particle of mass M such that the second particle starts moving and the first particle stops just after the collision. Then which of the following conditions must always be valid ?
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution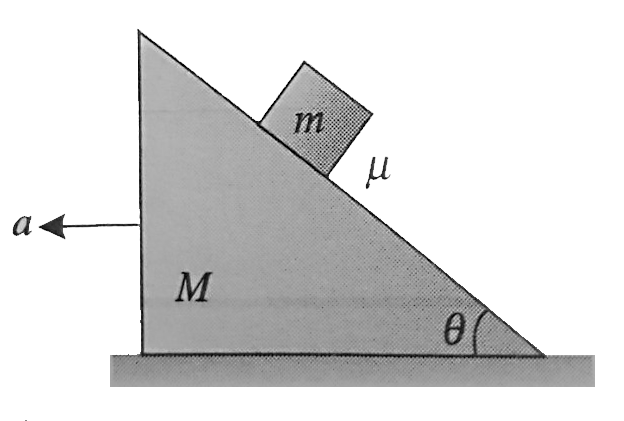
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionA sphere P of mass m moving with velocity u collides head on with another sphere Q of mass m which is at rest . The ratio of final velocity of Q to initial velocity of P is
( e = coefficient of restitution )
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View Solution
