A block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
To solve the problem step by step, we will analyze the collision between the two blocks and apply the principles of conservation of momentum and the definition of the coefficient of restitution.
Step 1: Identify the given data
- Mass of the first block (m) = m
- Initial speed of the first block (u₁) = v
- Mass of the second block (2m) = 2m
- Initial speed of the second block (u₂) = 0 (at rest)
- Final speed of the first block after collision (v₁) = 0 (comes to rest)
Step 2: Apply the conservation of momentum
The total momentum before the collision must equal the total momentum after the collision.
Initial momentum (P_initial):
Pinitial=m⋅u1+2m⋅u2=m⋅v+2m⋅0=mv
Final momentum (P_final):
Let the final speed of the second block (2m) be v₂.
Pfinal=m⋅v1+2m⋅v2=m⋅0+2m⋅v2=2mv2
Setting initial momentum equal to final momentum:
mv=2mv2
Step 3: Solve for the final velocity of the second block
Dividing both sides by m (assuming m ≠ 0):
v=2v2
Now, solving for v₂:
v2=v2
Step 4: Calculate the coefficient of restitution (e)
The coefficient of restitution (e) is defined as the ratio of the relative speed of separation to the relative speed of approach.
Velocity of separation:
Velocity of separation=v2−v1=v2−0=v2
Velocity of approach:
Velocity of approach=u1−u2=v−0=v
Now, substituting these values into the formula for e:
e=Velocity of separationVelocity of approach=v2v
Step 5: Simplify the expression for e
e=12
Final Answer
The coefficient of restitution (e) is 12 or 0.5.
---
- Mass of the first block (m) = m
- Initial speed of the first block (u₁) = v
- Mass of the second block (2m) = 2m
- Initial speed of the second block (u₂) = 0 (at rest)
- Final speed of the first block after collision (v₁) = 0 (comes to rest)
The total momentum before the collision must equal the total momentum after the collision.
Pinitial=m⋅u1+2m⋅u2=m⋅v+2m⋅0=mv
Let the final speed of the second block (2m) be v₂.
Pfinal=m⋅v1+2m⋅v2=m⋅0+2m⋅v2=2mv2
mv=2mv2
Dividing both sides by m (assuming m ≠ 0):
v=2v2
v2=v2
The coefficient of restitution (e) is defined as the ratio of the relative speed of separation to the relative speed of approach.
Velocity of separation=v2−v1=v2−0=v2
Velocity of approach=u1−u2=v−0=v
e=Velocity of separationVelocity of approach=v2v
e=12
The coefficient of restitution (e) is 12 or 0.5.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - worked out Examples
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionAn object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.
View SolutionAn object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.
View SolutionBody A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View Solution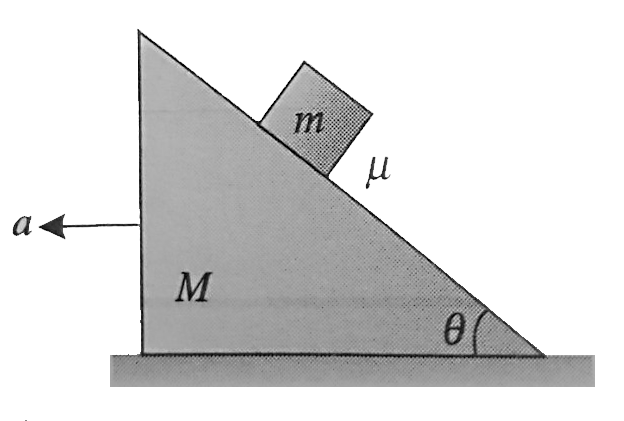
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionA moving block having mass m , collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the block is v, then the value of coefficient of restitution (e) will be
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View Solution
