A moving body can be stopped by a force F in time t. How much force will be needed to stop the body in half the time, when its momentum is doubled?
As F=change in momentumtime taken, therefore,
when momentum is doubled and time is halved, force F needed would become 4 times.
Topper's Solved these Questions
- FORCES AND LAWS OF MOTIONBOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
28 Videos
- FORCES AND LAWS OF MOTIONBOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MOCK TEST
36 Videos
- FORCES AND LAWS OF MOTIONBOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - WORKSHEET TESTING
11 Videos
- FLOTATIONBOOK - PRADEEPCHAPTER - FLOTATIONEXERCISE - Problem For Practice
6 Videos
- GRAVITATIONBOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Model Test paper (1)
36 Videos
Similar Questions
A body of mass 0.25 kg moving with velocity 12m/s is stopped by applying a force of 0.6 N. Calculate the time taken to stop the body. Also calculate the impulse of this force.
View SolutionForce acting on a body varies with time as shown below. If initial momentum of the body is →p, then the time taken by the body to retain its momentum →p again is

View Solution
Knowledge Check
A moving body cannot stop on its own. This is due to
Ainertia of restBinertia of motionCinertia of directionDall of theese.When a moving body is suddenly stopped
Africtional force increases.Bfrictional force gradually reduces to one.Cfrictional force becomes infinite.Dthe frictional force reduces to zero as it is a self adjusting force.How much force acts on a body whose momentum is constant
AzeroBp/2tC2p/tDnone of these
A body stops after some time. What is zero ?
View SolutionIf the speed of a motor car is doubled , how much more distance will it cover before stopping under the same retarding force ?
View SolutionA body of mass 5 kg is acted upon by a net force F which varies with time t as shown in graph, then the net momentum in SI units gained by the body at the end of 10 seconds is

View SolutionThe product of force and the time for which the force acts on a body is equal to the change in ______ of the body.
View SolutionA body of mass 10 kg is acted upon by a net force F which varies with time t as shown in figure. Then the net momentum in SI units gained by the body at the end of 10 seconds is
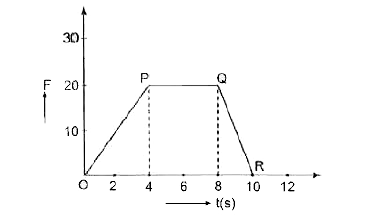
View Solution
