A musical scale that is not based on any one key-note but has the same character independent of the starting note is known as an equally tempered scale. If in this scale, an octave is divided into 12 half tones, what are the frequencies of the successive half-tones between a note of frequency 256 Hz and its octave ?
To find the frequencies of the successive half-tones between a note of frequency 256 Hz and its octave (512 Hz) in an equally tempered scale, we can follow these steps:
Step 1: Understand the relationship between frequencies in an octave
In an equally tempered scale, an octave is divided into 12 equal parts (half-tones). The frequency of the note after one octave is double the frequency of the starting note. Therefore, if the starting frequency is f0=256 Hz, the frequency of the octave is:
foctave=2×f0=2×256=512 Hz
Step 2: Determine the frequency ratio for each half-tone
The frequency ratio P between successive half-tones can be found using the formula:
foctave=f0×P12
Substituting the known values:
512=256×P12
Step 3: Solve for P12
Rearranging the equation gives:
P12=512256=2
Step 4: Take the logarithm of both sides
Taking the logarithm of both sides, we have:
log(P12)=log(2)
Using the property of logarithms:
12log(P)=log(2)
Step 5: Solve for log(P)
Now, we can solve for log(P):
log(P)=log(2)12
Using the approximate value of log(2)≈0.301:
log(P)≈0.30112≈0.0251
Step 6: Calculate P
Now, we can find P by taking the antilogarithm:
P≈100.0251≈1.06
Step 7: Calculate the frequencies of successive half-tones
The frequencies of the successive half-tones can be calculated using the formula:
fn=f0×Pn
where n is the number of half-tones.
- For n=1:
f1=256×1.061≈271.36 Hz
- For n=2:
f2=256×1.062≈287.73 Hz
- For n=3:
f3=256×1.063≈304.56 Hz
Continuing this process up to n=12:
- For n=12:
f12=256×1.0612≈512 Hz
Final Frequencies
Thus, the frequencies of the successive half-tones from 256 Hz to 512 Hz are approximately:
- f1≈271.36 Hz
- f2≈287.73 Hz
- f3≈304.56 Hz
- ...
- f12=512 Hz
In an equally tempered scale, an octave is divided into 12 equal parts (half-tones). The frequency of the note after one octave is double the frequency of the starting note. Therefore, if the starting frequency is f0=256 Hz, the frequency of the octave is:
foctave=2×f0=2×256=512 Hz
The frequency ratio P between successive half-tones can be found using the formula:
foctave=f0×P12
Substituting the known values:
512=256×P12
Rearranging the equation gives:
P12=512256=2
Taking the logarithm of both sides, we have:
log(P12)=log(2)
Using the property of logarithms:
12log(P)=log(2)
Now, we can solve for log(P):
log(P)=log(2)12
Using the approximate value of log(2)≈0.301:
log(P)≈0.30112≈0.0251
Now, we can find P by taking the antilogarithm:
P≈100.0251≈1.06
The frequencies of the successive half-tones can be calculated using the formula:
fn=f0×Pn
where n is the number of half-tones.
f1=256×1.061≈271.36 Hz
f2=256×1.062≈287.73 Hz
f3=256×1.063≈304.56 Hz
- For n=12:
f12=256×1.0612≈512 Hz
Thus, the frequencies of the successive half-tones from 256 Hz to 512 Hz are approximately:
- f1≈271.36 Hz
- f2≈287.73 Hz
- f3≈304.56 Hz
- ...
- f12=512 Hz
Topper's Solved these Questions
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Musical Sound
2 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Conceptual Short Answer Questions With Answers
25 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Additional Solved Problems
13 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
Knowledge Check
A musical scale is constructed by providing intermediate frequencies between a note and its octave which
Aform an arithmetic progressionBform a geometric progressionCbear a simple ratio with their neighboursDform a harmonic progression
What is the percentage change in the tension necessary in a sonometer of fixed length to produce a note one octave lower (half of original frequency) than before?
View SolutionIn certain ranges of a piano keyboard , more than one string is tuned to the same note to provide extra loudness . For example , the note at 110Hz has two strings at this frequency . If one string slips from its normal tension of 600Nto540N , what beat frequency is heard when the hammer strikes the two strings simultaneously ?
View SolutionWhen Farmer Oak smiled, the corners of his mouth spread till they were within an unimportant distance of his ears, his eyes were reduced to chinks, and diverging wrinkles appeared round them, extending upon his countenance like the rays in a rudimentary sketch of the rising sun.
His Christian name was Gabriel, and on working days he was a young man of sound judgment, easy motions, proper dress, and general good character. On Sundays he was a man of misty views, rather given to postponing, and hampered by his best clothes and umbrella: upon the whole, one who felt himself to occupy morally that vast middle space of Laodicean neutrality which lay between the Communion people of the parish and the drunken section,- that is, he went to church, but yawned privately by the time the congregation reached the Nicene creed, and thought of what there would be for dinner when he meant to be listening to the sermon. Or, to state his character as it stood in the scale of public opinion, when his friends and critics were in tantrums, he was considered rather a bad man, when they were pleased, he was rather a good man, when they were neither, he was a man whose moral colour was a kind of pepper and salt mixture.
Since he lived six times as many working-days as Sundays, Oak's appearance in his old clothes was most peculiarly his own-the mental picture formed by his neighbours in imagining him being always dressed in that way. He wore a low-crowned felt hat, spread out at the base by tight jamming upon the head for security in high winds, and a coat like Dr. Johnson's, for his lower extremities being encased in ordinary leather leggings and boots emphatically large, affording to each foot a roomy apartment so constructed that any wearer might stand in a river all day long and know nothing of damp-their maker being a conscientious man who endeavoured to compensate for any weakness in his cut by unstinted dimension and solidity.
Mr. Oak carried about him, by way of watch, what may be called a small silver clock, in other words, it was a watch as to shape and intention, and a small clock as to size. This instrument being several years older than Oak's grandfather had the peculiarity of going either too fast or not at all. The smaller of its hands, too, occasionally slipped round on the pivot, and thus, though the minutes were told with precision, nobody could be quite certain of the hour they belonged to. The stopping peculiarity of his watch Oak remedied by thumps and shakes, and he escaped any evil consequences from the other two defects by constant comparisons with and observations of the sun and stars, and by pressing his face close to the glass of his neighbours' windows, till he could discern the hour marked by the green-faced timekeepers within. It may be mentioned that Oak's fob being difficult of access, by reason of its somewhat high situation in the waistband of his trousers (which also lay at a remote height under his waistcoat), the watch was as a necessity pulled out by throwing the body to one side, compressing the mouth and face to a mere mass of ruddy flesh on account of the exertion, and drawing up the watch by its chain, like a bucket from a well.
[From "Far From the Madding Crowd', by Thomas Hardy]
For each word given below choose the correct meaning (as used in the passage) from the options provided:
diverging
View SolutionWhen Farmer Oak smiled, the corners of his mouth spread till they were within an unimportant distance of his ears, his eyes were reduced to chinks, and diverging wrinkles appeared round them, extending upon his countenance like the rays in a rudimentary sketch of the rising sun.
His Christian name was Gabriel, and on working days he was a young man of sound judgment, easy motions, proper dress, and general good character. On Sundays he was a man of misty views, rather given to postponing, and hampered by his best clothes and umbrella: upon the whole, one who felt himself to occupy morally that vast middle space of Laodicean neutrality which lay between the Communion people of the parish and the drunken section,- that is, he went to church, but yawned privately by the time the congregation reached the Nicene creed, and thought of what there would be for dinner when he meant to be listening to the sermon. Or, to state his character as it stood in the scale of public opinion, when his friends and critics were in tantrums, he was considered rather a bad man, when they were pleased, he was rather a good man, when they were neither, he was a man whose moral colour was a kind of pepper and salt mixture.
Since he lived six times as many working-days as Sundays, Oak's appearance in his old clothes was most peculiarly his own-the mental picture formed by his neighbours in imagining him being always dressed in that way. He wore a low-crowned felt hat, spread out at the base by tight jamming upon the head for security in high winds, and a coat like Dr. Johnson's, for his lower extremities being encased in ordinary leather leggings and boots emphatically large, affording to each foot a roomy apartment so constructed that any wearer might stand in a river all day long and know nothing of damp-their maker being a conscientious man who endeavoured to compensate for any weakness in his cut by unstinted dimension and solidity.
Mr. Oak carried about him, by way of watch, what may be called a small silver clock, in other words, it was a watch as to shape and intention, and a small clock as to size. This instrument being several years older than Oak's grandfather had the peculiarity of going either too fast or not at all. The smaller of its hands, too, occasionally slipped round on the pivot, and thus, though the minutes were told with precision, nobody could be quite certain of the hour they belonged to. The stopping peculiarity of his watch Oak remedied by thumps and shakes, and he escaped any evil consequences from the other two defects by constant comparisons with and observations of the sun and stars, and by pressing his face close to the glass of his neighbours' windows, till he could discern the hour marked by the green-faced timekeepers within. It may be mentioned that Oak's fob being difficult of access, by reason of its somewhat high situation in the waistband of his trousers (which also lay at a remote height under his waistcoat), the watch was as a necessity pulled out by throwing the body to one side, compressing the mouth and face to a mere mass of ruddy flesh on account of the exertion, and drawing up the watch by its chain, like a bucket from a well.
[From "Far From the Madding Crowd', by Thomas Hardy]
For each word given below choose the correct meaning (as used in the passage) from the options provided:
postponing
View SolutionWhen Farmer Oak smiled, the corners of his mouth spread till they were within an unimportant distance of his ears, his eyes were reduced to chinks, and diverging wrinkles appeared round them, extending upon his countenance like the rays in a rudimentary sketch of the rising sun.
His Christian name was Gabriel, and on working days he was a young man of sound judgment, easy motions, proper dress, and general good character. On Sundays he was a man of misty views, rather given to postponing, and hampered by his best clothes and umbrella: upon the whole, one who felt himself to occupy morally that vast middle space of Laodicean neutrality which lay between the Communion people of the parish and the drunken section,- that is, he went to church, but yawned privately by the time the congregation reached the Nicene creed, and thought of what there would be for dinner when he meant to be listening to the sermon. Or, to state his character as it stood in the scale of public opinion, when his friends and critics were in tantrums, he was considered rather a bad man, when they were pleased, he was rather a good man, when they were neither, he was a man whose moral colour was a kind of pepper and salt mixture.
Since he lived six times as many working-days as Sundays, Oak's appearance in his old clothes was most peculiarly his own-the mental picture formed by his neighbours in imagining him being always dressed in that way. He wore a low-crowned felt hat, spread out at the base by tight jamming upon the head for security in high winds, and a coat like Dr. Johnson's, for his lower extremities being encased in ordinary leather leggings and boots emphatically large, affording to each foot a roomy apartment so constructed that any wearer might stand in a river all day long and know nothing of damp-their maker being a conscientious man who endeavoured to compensate for any weakness in his cut by unstinted dimension and solidity.
Mr. Oak carried about him, by way of watch, what may be called a small silver clock, in other words, it was a watch as to shape and intention, and a small clock as to size. This instrument being several years older than Oak's grandfather had the peculiarity of going either too fast or not at all. The smaller of its hands, too, occasionally slipped round on the pivot, and thus, though the minutes were told with precision, nobody could be quite certain of the hour they belonged to. The stopping peculiarity of his watch Oak remedied by thumps and shakes, and he escaped any evil consequences from the other two defects by constant comparisons with and observations of the sun and stars, and by pressing his face close to the glass of his neighbours' windows, till he could discern the hour marked by the green-faced timekeepers within. It may be mentioned that Oak's fob being difficult of access, by reason of its somewhat high situation in the waistband of his trousers (which also lay at a remote height under his waistcoat), the watch was as a necessity pulled out by throwing the body to one side, compressing the mouth and face to a mere mass of ruddy flesh on account of the exertion, and drawing up the watch by its chain, like a bucket from a well.
[From "Far From the Madding Crowd', by Thomas Hardy]
For each word given below choose the correct meaning (as used in the passage) from the options provided:
compensate
View Solution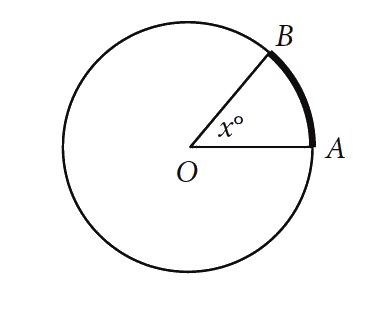
Note: Figure not drawn to scale.
In the figure above, the circle has center O and has radius 10. If the length of arc (shown in bold) is between 5 and 6, what is one possible integer–––––––– value of x ?
(shown in bold) is between 5 and 6, what is one possible integer–––––––– value of x ?
View SolutionA string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of 100Hz. What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibratin ?
View Solution
