The 6563 Ã… Hα line emitted by hydrogen in a star is found to be red-shifted by 15 Ã…. The speed with which the star is receding from the earth is
λ=6563A=6563×10−10m,△λ=15A,c=3×108m/s
Frequency shift △v=v.−v=−Vvc
v=cλ,△v=−cλ2△λ
−cλ2△x=−Vvc
V=c△λλ=3×108×15×10−106563×10−10=6.86×105m/s
Topper's Solved these Questions
- BOOK - ICSECHAPTER - WAVESEXERCISE - Musical Sound2videos
WAVES
- BOOK - ICSECHAPTER - WAVESEXERCISE - Conceptual Short Answer Questions With Answers25videos
WAVES
- BOOK - ICSECHAPTER - WAVESEXERCISE - Additional Solved Problems13videos
WAVES
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS79videos
VECTORS SCALARS ELEMENTARY CALCULUS
Similar Questions
The 6563ÅH2 line emitted by hydrogen in a star is found to be red shifted by 15Å. Estimate the speed with which the star is receding from earth.
View SolutionThe 6563 Å line emitted by hydrogen atom in a star is found to be red shifted by 5 Å. The speed with which the star is receding form the earth is
View Solution
Knowledge Check
- Question 1 - Select One
The 6563ÅH2 line emitted by hydrogen in a star is found to be red shifted by 15Å. Estimate the speed with which the star is receding from earth.
A3.2×105ms−1B6.87×105ms−1C2×105ms−1D12.74×105ms−1 - Question 2 - Select One
If a star is moving towards the earth, then the lines are shifted towards
AredBinfra-redCblueDgreen - Question 3 - Select One
The wavelength of spectral line coming from a distant star shifts from 600 nm to 600.1 nm. The velocity of the star relative to earth is
A50 km s−1B100 km s−1C25 km s−1D200 km s−1
A 6000 Å Hβ line emitted by hydrogen in a star is observed to be red shifted by 10 Å. Find the speed with which star is receding away from the earth.
View SolutionThe wavelength of Hα line in the hydrogen spectrum is found to be 6563Å in the laboratory. If the velocity of the milky way is 1.05×106ms−1, then the wavelength of Hα line in the spectrum of milky way will be
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
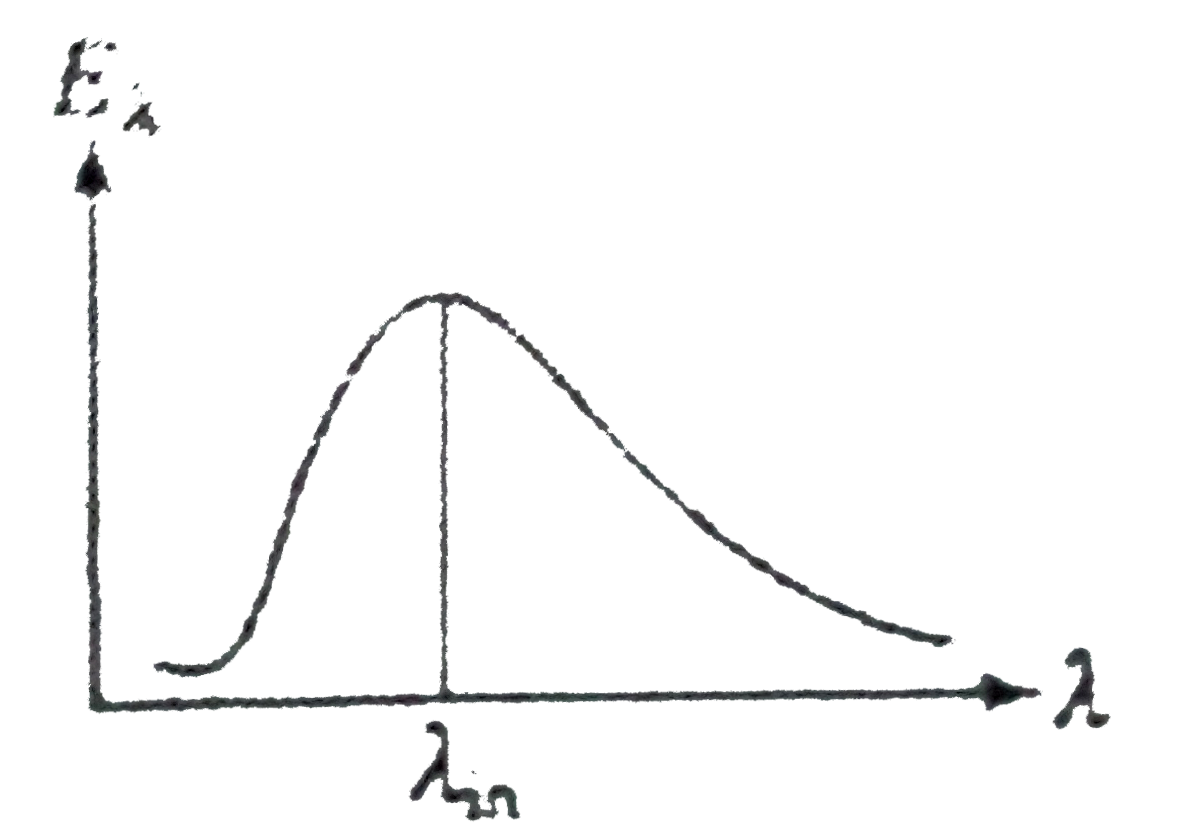
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) isView SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
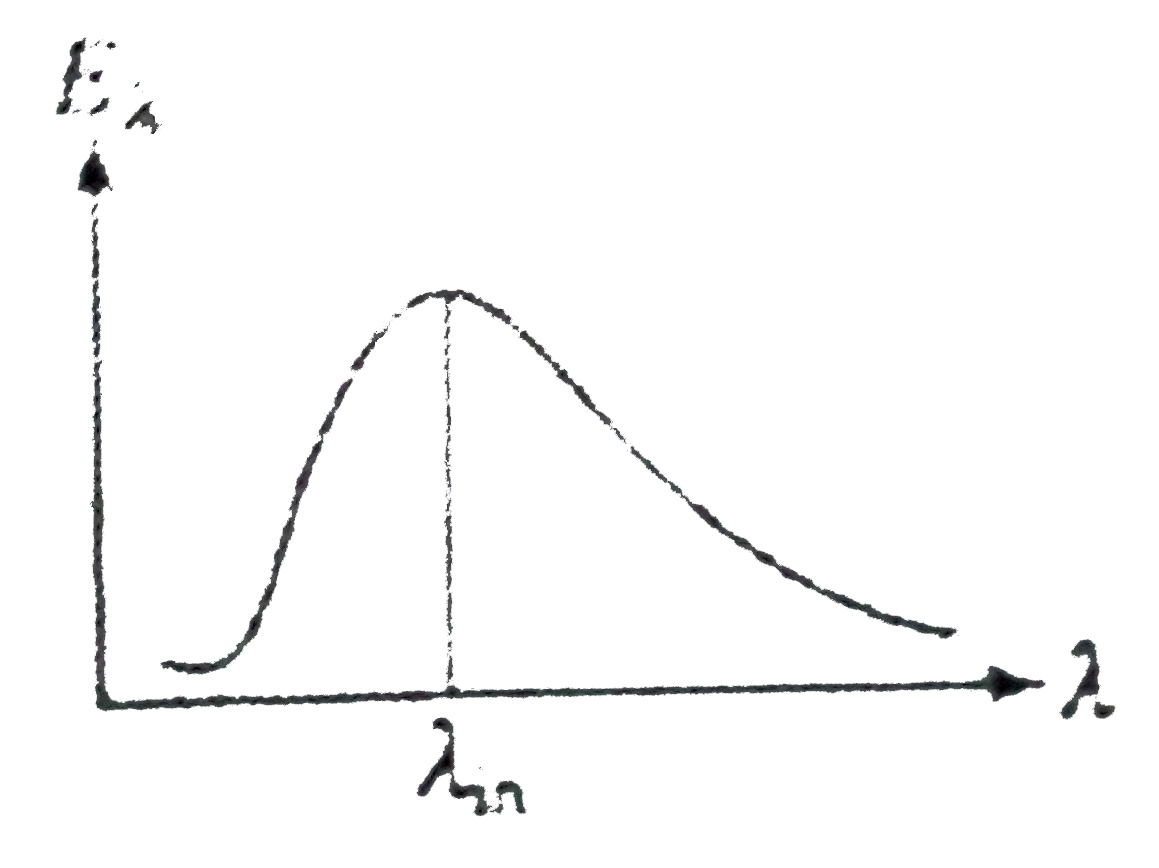
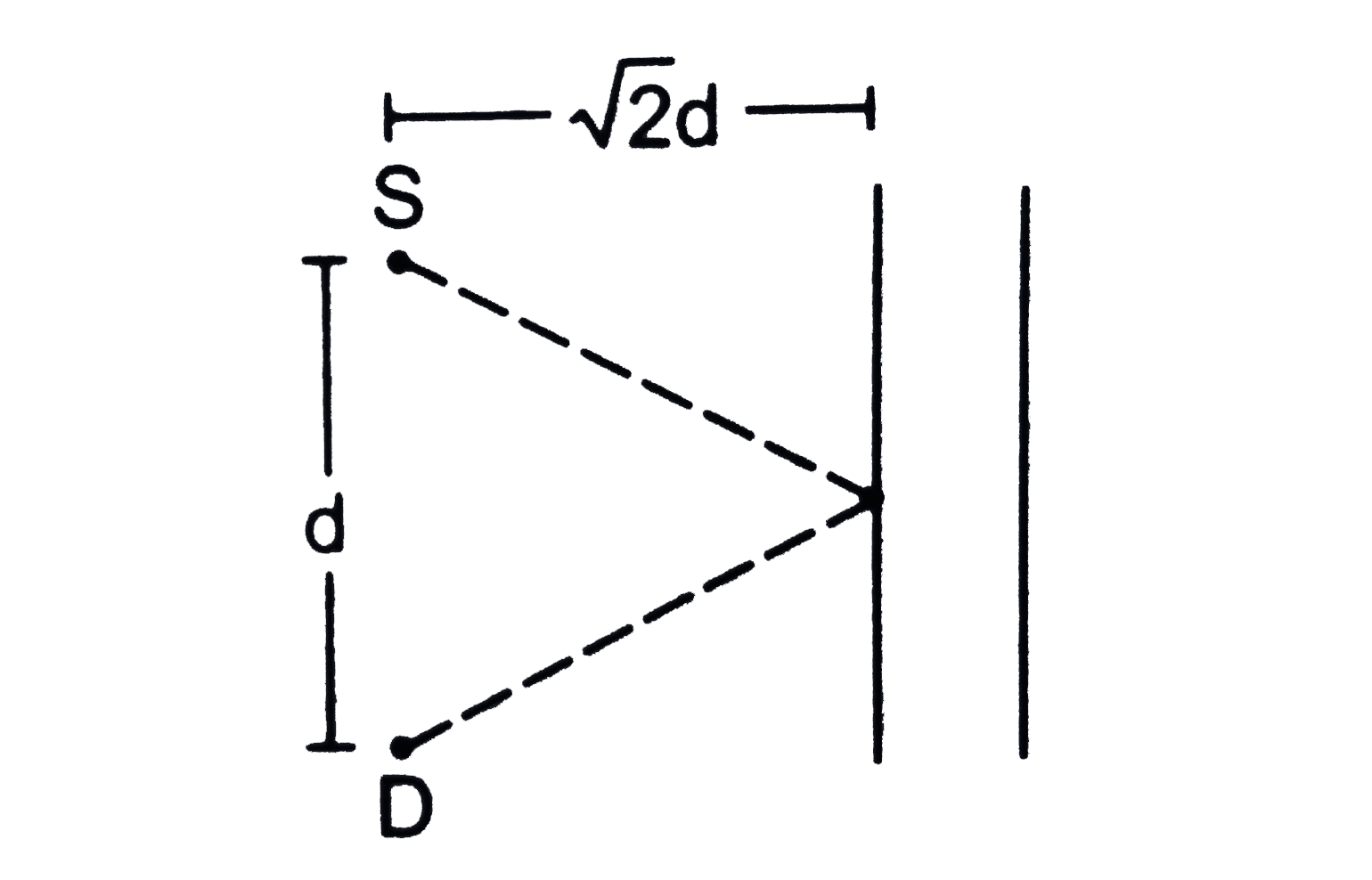
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
 View Solution
View Solution

