A narrow monochromatic beam of light of intensity 1 is incident on a glass plate as shown in figure Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects $25 %$ of the light incident on it and transmits intensities in the interference pattern formed by two beams obtained after one reflection at each plate.

Video Solution

Text Solution

Verified by Experts

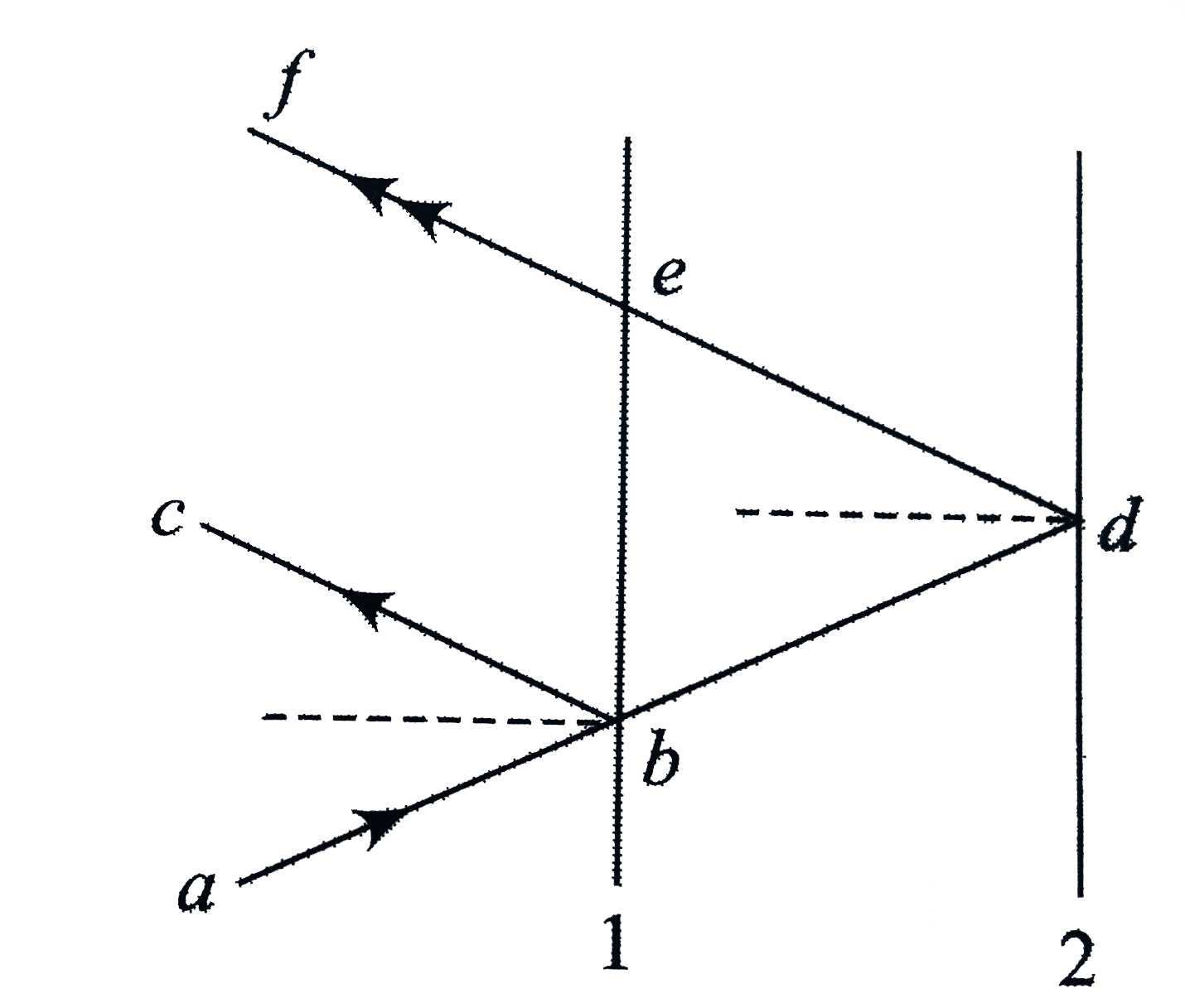
Let $I$ be the intensity of beam no. $1$ incident on first glass plate. Fig. It is partially reflected and partially transmitted. As each plate reflects $25 %$ of light falling on it and transmits $75 %$ . therefore, as is clear from Fig.
$I_{2} = \frac{25}{100} I = \frac{I}{4}$ $I_{3} = \frac{75}{100} I = \frac{3}{4} I$
$I_{4} = \frac{25}{100} I_{3} = \frac{1}{4} \times \frac{3}{4} = \frac{3}{16} I$ $I_{5} = \frac{75}{100} I_{4} = \frac{3}{4} \times \frac{3}{16} I = \frac{9}{64} I$
If $a$ and $b$ are amplitude of beam $I_{2}$ and $I_{5}$ .
when $I_{2} = \frac{I}{4} = K a^{2}$ or $a = \sqrt{\frac{I}{4 K}} = \frac{1}{2} \sqrt{\frac{I}{K}}$
$I_{5} = \frac{9}{64} I = K b^{2}$ or $b = \sqrt{\frac{9 I}{64 K}} = \frac{3}{8} \sqrt{\frac{1}{K}}$
$\frac{I_{min}}{I_{max}} = \frac{{(a - b)}^{2}}{{(a + b)}^{2}} = \frac{{(\frac{1}{2} - \frac{3}{8})}^{2} I / K}{{(\frac{1}{2} + \frac{3}{8})}^{2} I / K} = \frac{{(\frac{1}{8})}^{2}}{{(\frac{7}{8})}^{2}} = \frac{1}{49}$