A neutral particle is initally at rest in a uniform magnetic field B as shown in the diagram. The particle then spontaneously decays into two fragments, one with a positive charge +q and mass 3m and the other with negative charge −q and mass m. Neglecting the interaction between the two charged particles and assuming that the speeds are much less than speed of light, determine the time (in μs) after the decay at which the two fragments first meet. (use the following data q=1μCB=2πμT,m=10−15kg). Both the charges have initial velocity in x−y plane.

250
500
600
750
The correct Answer is:D
Initial momentum (p) of them all be same but opposite direction.
R=pqB = same for both.
Let they meet at angle θ, at time t. Then
Rθ=v0t.....(i)
and R(2π−θ)=3v0t.....(ii)
from (i) and (ii), t=πR2v0=π2v0=π2v03mv0qB
=3πm2qB=3π×10−152×10−6×2π×10−6

=34×10−3s=750μs
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - AIPMTNEET Questions
47 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
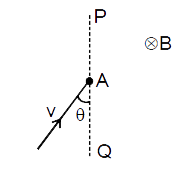
time spent
View SolutionA neutral particle is at rest in a uniform magnetic field →B.At t=0,particle decays into two particles each of mass m and one of them having charge q Both of these move off in separate paths lying in plane perpendicular to →B.A later time,the particles collide.Find this time of collision neglecting the interaction force.
View Solution
Knowledge Check
A neutral particle at rest in a magnetic field decays into two charged particles of different mass. The energy released goes into their kinetic energy. Then what can be the path of the particles. Neglect any interaction between the two charges.
A B
B C
C D
D
A charged particle of charge q and mass m enters a magnetic field as shown. Find radius of the circular path and the time spent inside the field. Neglect gravity.
 ARπθvBR(π−2θ)vCR(π+2θv)D2Rθv
ARπθvBR(π−2θ)vCR(π+2θv)D2RθvA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
A4πr2Bμ0uB2πr2Bμ0uCmuBrD2muBr
A charged particle having charge q is moving in a uniform magnetic field B parallel to the lines of field force, the magnetic force acting on a charge will be qvB
View SolutionA neutral particle is at rest in a uniform magnetic field B. At time t=0 it decays into two charged particles, each of mass m.
(a) If the charge of one of the particles is +q, what is the charge of the other?
(b) The two particles move off in separate paths, both of them lie in the plane perpendicular to B. At a later time, the particles collide. Express the time from decay until collision in terms of m,B and q.
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View Solution
