A non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
Charge on the differntial circular
strip is
dq=(2πRsinθ)(Rdθ)σ
⇒dq=2πσR2sinθdθ,
dI=ωdq2π=ωσR2sinθdθ
(a) Magnetic field at the centre is
dB=μ0dI(R2sin2θ)2R3
μ0ωσRsin3θdθ2
B=μ0ωσR2∫π0sin3θdθ=μ0ωσR∫π/20sin3θdθ
⇒→B=23μ0ωσR(ˆk) [∵sin3θ=14(3sinθ−sin3θ)]
(b) Magnetic moment due to elementary ring, dμ=(dI)πr2
μ=∫(dI)πr2=2∫π/20(ωσR2sinθ)πR2sin2θdθ
=2πR4ωσ∫π/20sin3θdθ=43πσR4ω
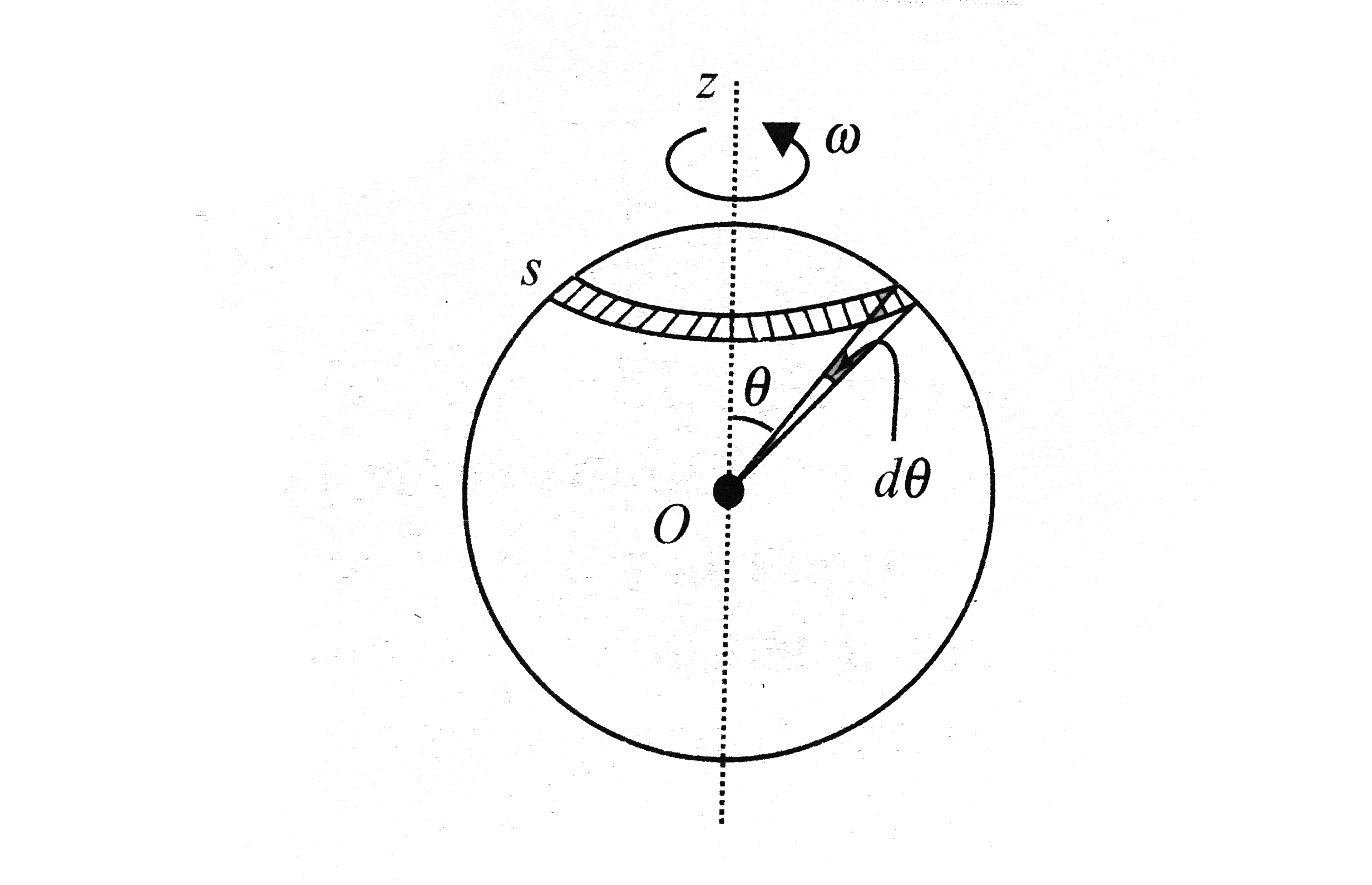
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density σ rotates about its axis with an angular velocity ω. Find :
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
( c) the ratio of magnetic moment and angular momentum of disc.View Solution
Knowledge Check
- Question 1 - Select One
A thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
AQR2ω8BQR2ω4CQR2ω2DZero - Question 2 - Select One or More
A non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.
 Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πR
Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πR
A non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
View SolutionA non-conducting sphere of radius R=50mm charged uniformly with surface density σ=10.0μC/m2 rotates with an angular velocity ω=70 rad/s about the asxis passign thorugh its centre. Find the magnetic induction at the centre of the sphere.
View SolutionA plastic disc of radius 'R' has a charge 'q' uniformly distributed over its surface. If the dis is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionA thin uniformring of radius R carrying uniform charge Q and mass M rotates about its axis with angular velocity ω. The ratio of its magnetic moment and angular momentum is:
View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density σ. About its central axis of rotation it rotates at an angular speed ω. Find the magnetic moment of disc due to rotation of charges.
View Solution

