A non-uniform bar of weight W and length L is suspended by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively.
The distance d of the centre of gravity of the bar from left end is.
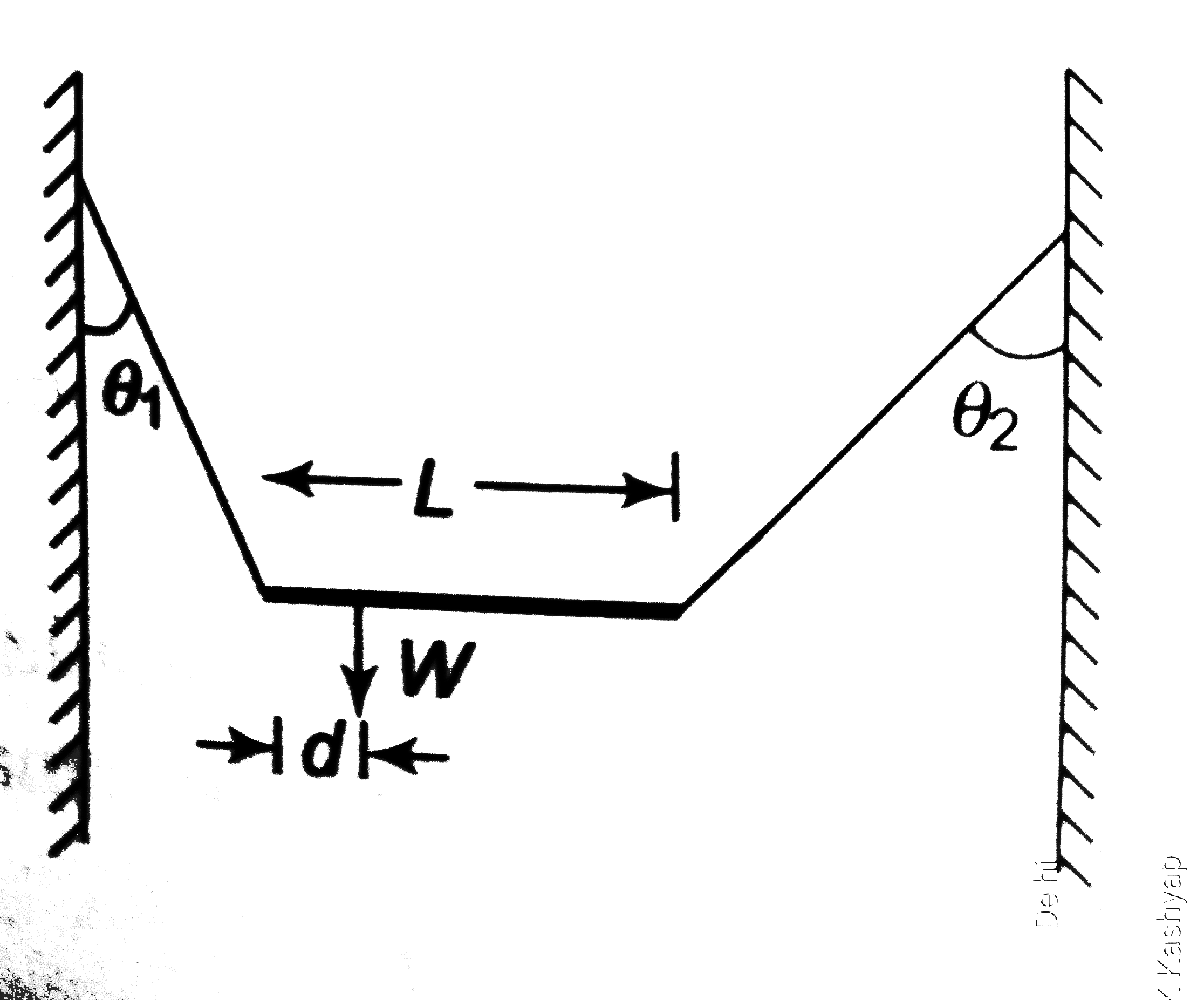 .
.
L(tanθ1+tanθ2tanθ1)
L(tanθ1tanθ1+tanθ2)
L(tanθ2tanθ1+tanθ2)
L(tanθ1+tanθ2tanθ2)
The correct Answer is:B
Let T1 and T2 be the tensions in two strings as shown in the figure.
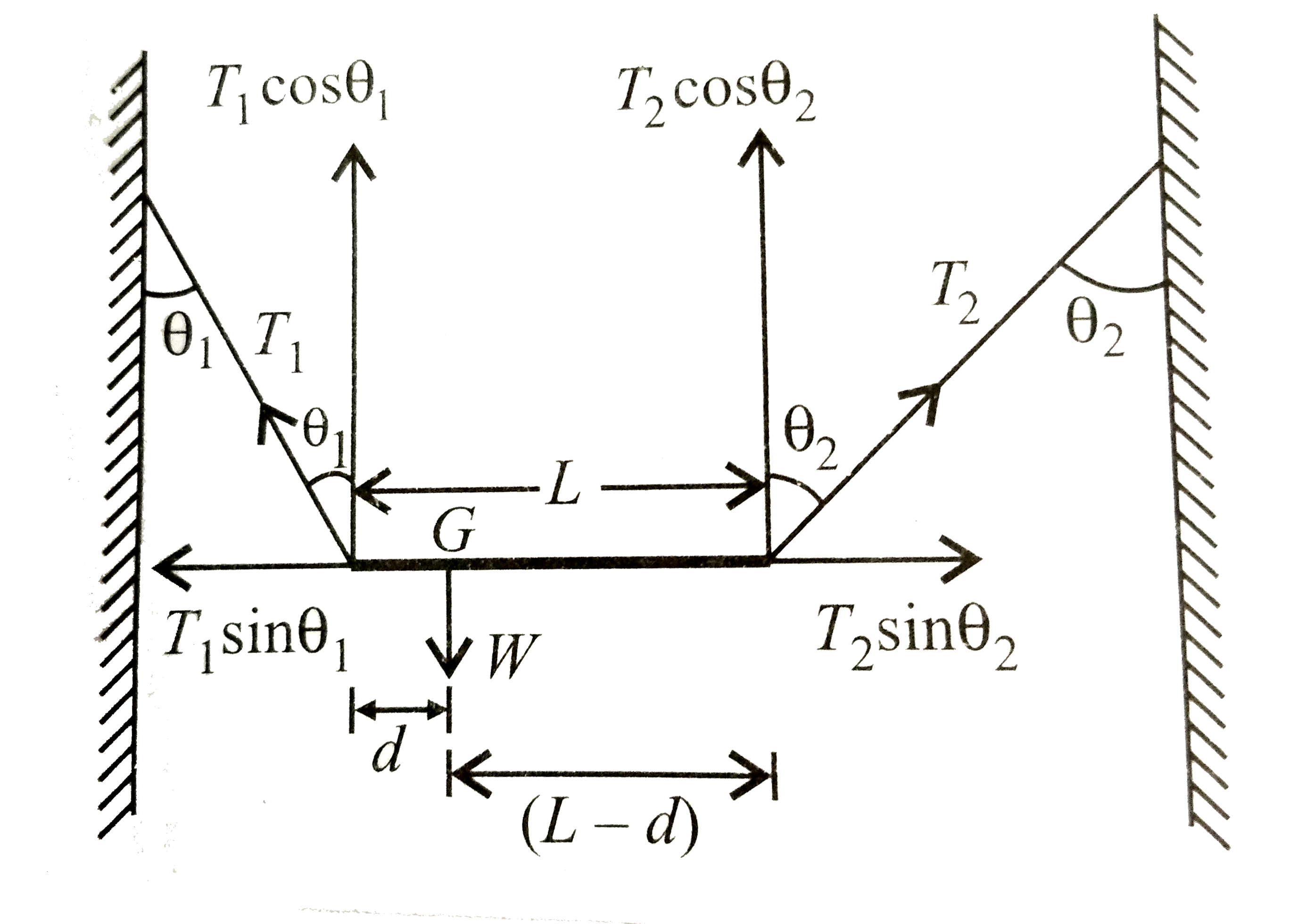
For translation equilibrium along the horizontal direction, we get
T1sinθ1=T2sinθ2
For rotational equilibrium about G
−T1sinθ1d+T2cosθ2(L−d)=0
T1cosθ1d=T2cosθ2(L−d)
Dividing equation (i) by (ii), we get
tanθ1d=tanθ2L−d or L−dd=tanθ2tanθ1
(Ld−1)=tanθ2tanθ1⇒Ld=tanθ2tanθ1+1
Ld=tanθ2+tanθ1tanθ1⇒d=Ltanθ1tanθ1+tanθ2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Moment Of Inertia
Explore 7 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Theorems Of Perpendicular And Parallel Axes
Explore 5 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Torque And Angular Momentum
Explore 11 Videos
- PRACTICE PAPERSBook:NCERT FINGERTIPSChapter:PRACTICE PAPERSExercise:Practice Paper 3
Explore 50 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTIPSChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9∘and53.1∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end.
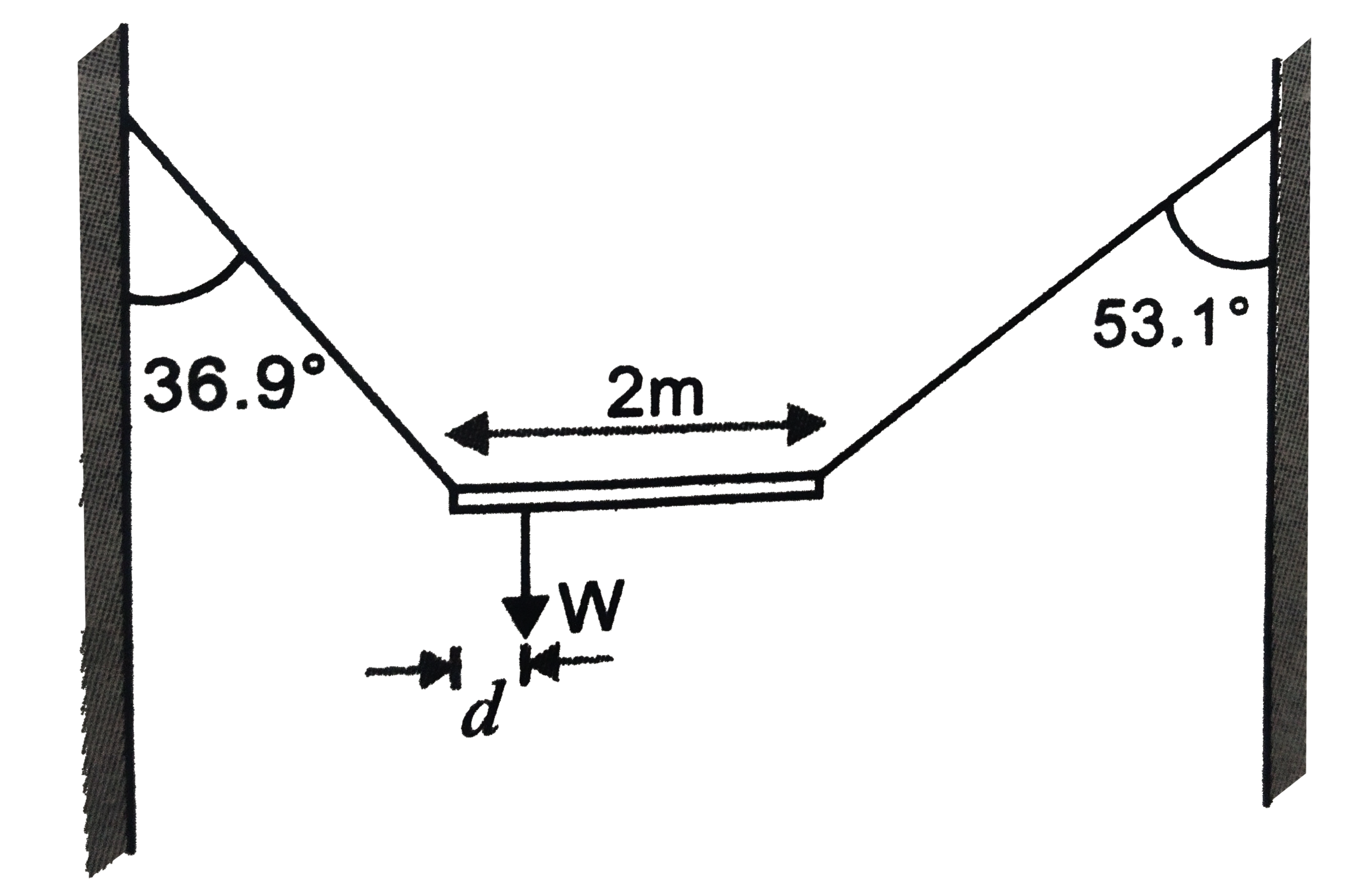
View SolutionA non-uniform bar of weight W is suspended at rest by two string of negligible weights as shown in figure. The angle made by the string with the vertical are 36.9∘ and 53.1∘ respectively. The bar 2m long. Calculate the distance of the centre of gravity (in cm ) of the bar from it left end.
'(##CEN_KSR_PHY_JEE_C09_E01_033_Q19##)'
View Solution
Knowledge Check
A non-uniform bar of weight W and weight L is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively.
The distance d of the centre of gravity of the bar from left end is.
 .AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)
.AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)A non-uniform bar of weight w is suspended at rest by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are 37∘ and 53∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end. given sin37∘=3/5 and sin53∘=4/5
 A72cmB64cmC100cmD40cm
A72cmB64cmC100cmD40cmA uniform rod of length l and mass m is suspended by two vertical inextensible strings as shwon in figure. Then, tension in the left string when right string snape, si
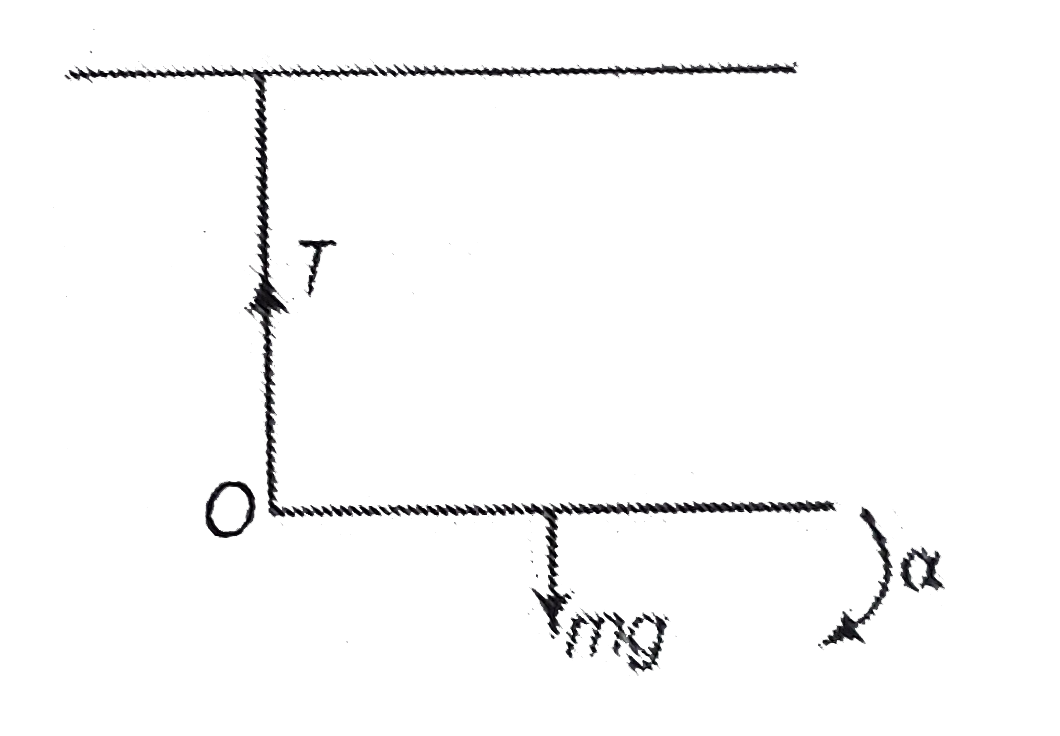 A3mg4Bmg4Cmg2Dmg8
A3mg4Bmg4Cmg2Dmg8
A uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is

View SolutionA uniform rod of length l and mass M is suspended on two vertical inextensible string as shown in figure. Then tension T in the left string at the instant, when right string snaps is?

View SolutionA uniform rod of mass and length l is suspended by two strings at its ends shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.
View SolutionA uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :

View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View Solution