A number of discs, each of momentum M kg m/s ar striking a wall at the rate of n discs per minute. The force associates with these discs, in newotns, would be
Mn60
60Mn
M60n
n60M
The correct Answer is:A
To find the force associated with the discs striking the wall, we can follow these steps:
1. Understanding the Problem:
We have discs each with momentum M (in kg m/s) striking a wall at a rate of n discs per minute. We need to calculate the force exerted by these discs on the wall.
2. Using the Concept of Force:
According to Newton's second law, force (F) is the rate of change of momentum (dpdt). Therefore, we can express the force as:
F=dpdt
3. Calculating the Change in Momentum:
Each disc has a momentum M. If n discs strike the wall per minute, the total momentum change per minute is:
Total momentum change=n×M
4. Converting Time Units:
Since the rate n is given per minute, we need to convert this rate into seconds. There are 60 seconds in a minute, so:
dt=160 minutes=1 minute=60 seconds
5. Calculating the Rate of Change of Momentum:
The rate of change of momentum per second (dpdt) can be calculated as:
dpdt=n×M60
6. Final Expression for Force:
Substituting this into the force equation gives:
F=n×M60
Thus, the force associated with the discs striking the wall is:
F=nM60 Newtons
Final Answer:
The force associated with these discs, in Newtons, would be nM60.
We have discs each with momentum M (in kg m/s) striking a wall at a rate of n discs per minute. We need to calculate the force exerted by these discs on the wall.
According to Newton's second law, force (F) is the rate of change of momentum (dpdt). Therefore, we can express the force as:
F=dpdt
Each disc has a momentum M. If n discs strike the wall per minute, the total momentum change per minute is:
Total momentum change=n×M
Since the rate n is given per minute, we need to convert this rate into seconds. There are 60 seconds in a minute, so:
dt=160 minutes=1 minute=60 seconds
The rate of change of momentum per second (dpdt) can be calculated as:
dpdt=n×M60
Substituting this into the force equation gives:
F=n×M60
F=nM60 Newtons
The force associated with these discs, in Newtons, would be nM60.
Topper's Solved these Questions
- LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEBOOK - MCGROW HILL PUBLICATIONCHAPTER - LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEEXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- HEATING AND MAGNETIC EFFECTS OF CURRENT BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATING AND MAGNETIC EFFECTS OF CURRENT EXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- MEASUREMENTBOOK - MCGROW HILL PUBLICATIONCHAPTER - MEASUREMENTEXERCISE - ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
13 Videos
Similar Questions
A gramophone disc is set revolving in a horizontal plane at the rate of 3312 revolutions per minute. It is found that a small coin placed on the disc will remain there if its centre is not more than 5 cm from the axis of rotation. Calculate the coefficient of friction between the coin and the disc
[Hint : Centripetal force =mω2r= Frictional force =μN=μmg]
View SolutionThree small discs are connected with two identical massless rods as shown in fig. The rods are pinned to the discs such that angle between them can change freely. The system is placed on a smooth horizontal surface with discs A and B touching a smooth wall and the angle ACB being 90∘. A force F is applied to the disc C in a direction perpendicular to the wall. Find acceleration of disc B immediately after the force starts to act. Masses of discs are mA=m,mB=2m,mC=m[ wall is perpendicular to the plane of the fig.]
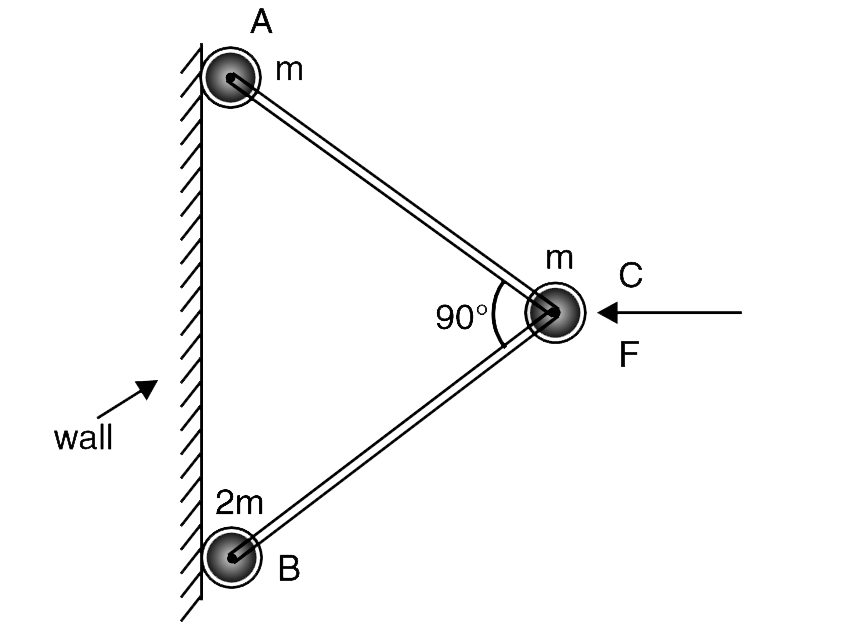
View Solution
Knowledge Check
A disc of radius 10 cm can rotate about an axis passing through its centre and perpendicular to its plane. A force of 10 N is applied along the tangent in the plane of the disc. If the moment of inertia of the disc about its centre is 5kgm2, then the increase in the angular velocity of the disc in 10 s will be
A2 rad/sB4 rad/sC1 rad/sD50 rad/sA unifrom disc is acted by two equal forces of magnitude F. One of them, acts tangentially to the disc, while other one is acting at the central point of the disc. The friction between disc surface and ground surface in nF. If r be the radius of the disc, then the value of n would be (in N)
A0B1.2C2.0D3.2A disc of moment of inertia 3kgm2 is acted upon by a constant torque of 60 Nm, if the disc is at rest, then the time after which the angular velocity of the disc is 90 rad/s, will be
A1.5 sB3 sC4.5 sD6 s
A disc A of mass m sliding over a smooth horizontal surface with velocity v experiences a perfectly elastic collision with a smooth stationary wall at a point O (figure). The angle between the motion direction of the disc and the normal of the wall is equal to α. Find:
(a) the points relative to which the angular momentum M of the disc remains constant in this process,
(b) the magnitude of the increment of the vector of the disc's angular momentum relative to the point O′ which is located in the plane of the disc's motion at the distance l from the point O.
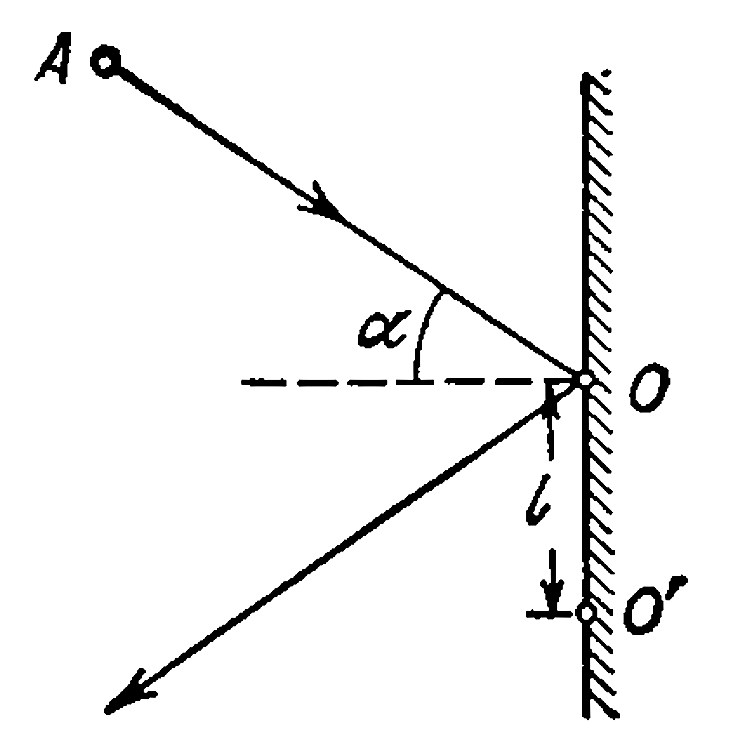
View SolutionA disc of mass m2 is placed on a table. A stiff spring is attached to it and is vertical. The other end of the spring is attached to a disc of mass m1 What minimum force should be applied to the upper disc to press the spring such that the lower disc is lifted off the table when the external force is suddenly removed?

View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
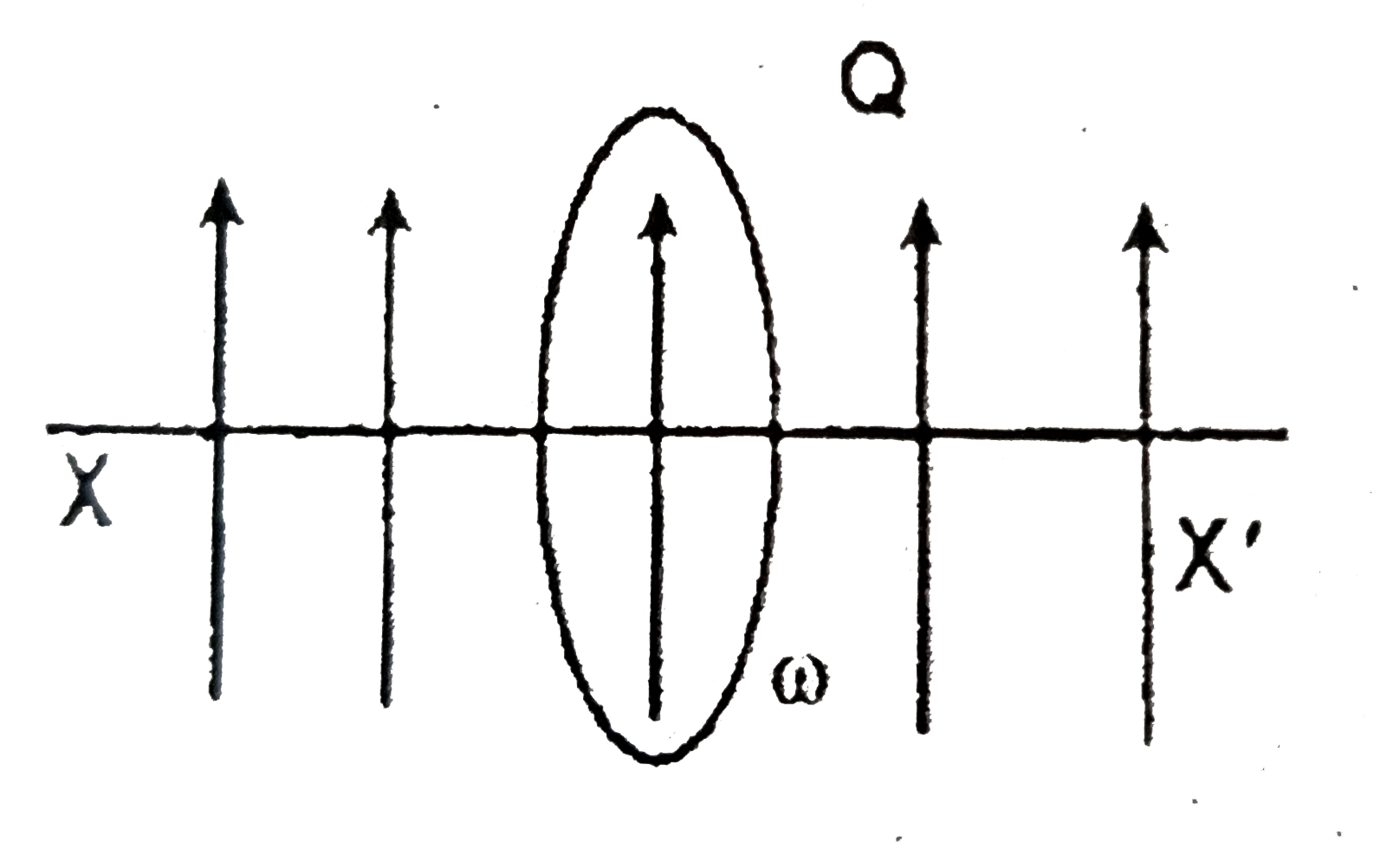
View Solution
